题目内容
8.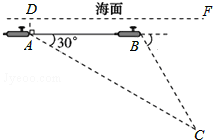 如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为55°.
如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为55°.(1)尺规作图:作点C到直线AB的垂线段CE(不写作法,保留作图痕迹);
(2)求海底C点处距离海面DF的深度.(结果精确到1米)
分析 (1)以C为圆心,合适的长度为半径作弧,交AB于M、N,分别以M、N为圆心作弧,交于H,连接CH交AB于E.
(2)依题意,AB=1000,∠EAC=30°,∠CBE=55°,设CD=x,则BE=x,进而利用正切函数的定义求出x即可.
解答  解:(1)如图,作CE⊥AB于E;
解:(1)如图,作CE⊥AB于E;
(2)依题意,AB=1464,∠EAC=30°,∠CBE=55°,
设CE=x,
在Rt△BCE中,cot55°=$\frac{BE}{CE}$,则BE=cot55°x,
Rt△ACE中,tan30°=$\frac{CE}{AE}$=$\frac{x}{1464+cot55°x}$=$\frac{\sqrt{3}}{3}$,
整理得出:3x=1464$\sqrt{3}$+$\sqrt{3}$x,
解得:x=732($\sqrt{3}$+1)≈2000米,
∴C点深度=x+600=2600米.
答:海底C点处距离海面DF的深度约为2600米.
点评 此题主要考查了俯角的定义及其解直角三角形的应用,解题时首先正确理解俯角的定义,然后利用三角函数和已知条件构造方程解决问题.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
13.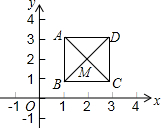 如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为( )
如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为( )
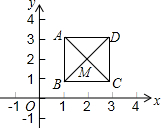 如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为( )
如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为( )| A. | (-2013,2) | B. | (-2013,-2) | C. | (-2014,-2) | D. | (-2014,2) |
20.下列各式中能用平方差公式计算的是( )
| A. | (-x+2y)(x-2y) | B. | (1-5m)(5m-1) | C. | (3x-5y)(3x+5y) | D. | (a+b)(-a-b) |
 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)C(8,0)D(8,8)抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)C(8,0)D(8,8)抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E