题目内容
8.如果圆环中大圆的半径为r,小圆的半径为$\frac{r}{2}$,则圆环的面积是$\frac{3}{4}$πr2.分析 直接利用大圆面积减去小圆面积进而得出答案.
解答 解:∵圆环中大圆的半径为r,小圆的半径为$\frac{r}{2}$,
∴圆环的面积是:π[r2-($\frac{r}{2}$)2]=$\frac{3}{4}$πr2.
故答案为:$\frac{3}{4}$πr2.
点评 此题主要考查了列代数式,正确表示出圆的面积是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.已知二次函数y=3(x-m)2+m+1的顶点在第二象限,则m的取值范围是( )
| A. | m>0 | B. | m<-1 | C. | -1<m<0 | D. | m>-1 |
13. 如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )
如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )
 如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )
如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )| A. | abc>0 | B. | a+b+c<0 | C. | b<a+c | D. | 4a+2b+c>0 |
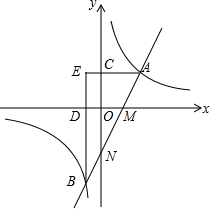 如图,直线y=2x-2分别与x轴、y轴相交于M,N两点,并且与双曲线y=$\frac{k}{x}$(k>0)相交于A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,AC与BD的延长线交于点E(m,n).
如图,直线y=2x-2分别与x轴、y轴相交于M,N两点,并且与双曲线y=$\frac{k}{x}$(k>0)相交于A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,AC与BD的延长线交于点E(m,n).