��Ŀ����
16��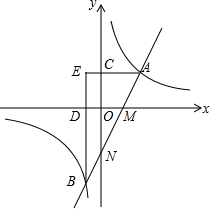 ��ͼ��ֱ��y=2x-2�ֱ���x�ᡢy���ཻ��M��N���㣬������˫����y=$\frac{k}{x}$��k��0���ཻ��A��B���㣬����A��AC��y���ڵ�C������B��BD��x���ڵ�D��AC��BD���ӳ��߽��ڵ�E��m��n����
��ͼ��ֱ��y=2x-2�ֱ���x�ᡢy���ཻ��M��N���㣬������˫����y=$\frac{k}{x}$��k��0���ཻ��A��B���㣬����A��AC��y���ڵ�C������B��BD��x���ڵ�D��AC��BD���ӳ��߽��ڵ�E��m��n������1����֤��$\frac{EC}{EA}$=$\frac{ED}{EB}$��
��2����$\frac{AM}{BM}$=$\frac{1}{2}$����$\frac{k}{x}$��2x-2��x��ȡֵ��Χ��
��3���ڣ�2���������£�PΪ˫������һ�㣬��OB��OPΪ�ڱ���ƽ���ı��Σ���ƽ���ı��ε��ܳ���С������ĸ�����Q�����꣮
���� ��1����A��x1��$\frac{k}{{x}_{1}}$����B��x2��$\frac{k}{{x}_{2}}$��������AE=x1-x2��BE=$\frac{k}{{x}_{1}}$-$\frac{k}{{x}_{2}}$��EC=-x2��ED=$\frac{k}{{x}_{1}}$������֤��$\frac{AE}{BE}$=$\frac{EC}{ED}$���ɴ˼��ɽ�����⣮
��2������DM��AE����$\frac{DE}{BD}$=$\frac{AM}{BM}$=$\frac{1}{2}$����A��m��n����B��-$\frac{m}{2}$��-2n������A��B����y=2x-2�õ�$\left\{\begin{array}{l}{n=2m-2}\\{-2n=4m-2}\end{array}\right.$�����$\left\{\begin{array}{l}{m=2}\\{n=2}\end{array}\right.$�����A��B�������꼴�ɽ�����⣮
��3����Ϊ��B�Ƕ��㣬OB�Ƕ���������Ҫ��ƽ���ı���OBPQ���ܳ�����Сֵֻ��Ҫ���OP����Сֵ���ɣ���P��y=$\frac{4}{x}$�ϣ���P��a��$\frac{4}{a}$������ΪOP2=n2+$\frac{16}{{n}^{2}}$=��n-$\frac{4}{n}$��2+8�����Ե�n-$\frac{4}{n}$=0ʱ��OP2��ֵ��С���ɴ˼��ɽ�����⣮
��� ��1��֤������A��x1��$\frac{k}{{x}_{1}}$����B��x2��$\frac{k}{{x}_{2}}$��������AE=x1-x2��BE=$\frac{k}{{x}_{1}}$-$\frac{k}{{x}_{2}}$��EC=-x2��ED=$\frac{k}{{x}_{1}}$��
��$\frac{AE}{BE}$=$\frac{{x}_{1}-{x}_{2}}{\frac{k}{{x}_{1}}-\frac{k}{{x}_{2}}}$=-$\frac{{x}_{1}{x}_{2}}{k}$��$\frac{EC}{ED}$=$\frac{-{x}_{2}}{\frac{k}{{x}_{1}}}$=-$\frac{{x}_{1}{x}_{2}}{k}$��
��$\frac{AE}{BE}$=$\frac{EC}{ED}$��
��$\frac{EC}{EA}$=$\frac{ED}{EB}$��
��2����DM��AE��
��$\frac{DE}{BD}$=$\frac{AM}{BM}$=$\frac{1}{2}$��
��A��m��n����B��-$\frac{m}{2}$��-2n����
��A��B����y=2x-2�õ�$\left\{\begin{array}{l}{n=2m-2}\\{-2n=4m-2}\end{array}\right.$��
���$\left\{\begin{array}{l}{m=2}\\{n=2}\end{array}\right.$��
��A��2��2����B��-1��-4����
��ͼ���֪��$\frac{k}{x}$��2x-2ʱ��x��-1��0��x��2��
��3���ɣ�2����֪��������������ʽΪy=$\frac{4}{x}$��A��2��2����B��1��-4����
���ı���OBPQ��ƽ���ı��Σ�
��OB=PQ��PO=BQ��
�ߵ�B�Ƕ��㣬��OB�Ƕ�����
��Ҫ��ƽ���ı���OBPQ���ܳ�����Сֵֻ��Ҫ���OP����Сֵ���ɣ�
��P��y=$\frac{4}{x}$�ϣ���P��a��$\frac{4}{a}$����
��OP2=n2+$\frac{16}{{n}^{2}}$=��n-$\frac{4}{n}$��2+8��
�൱n-$\frac{4}{n}$=0ʱ��OP2��ֵ��С��
��n=��2ʱ��OP����Сֵ��
��P��2��2����-2��-2����Q��1��-2����-3��-6����
���� ���⿼�鷴���������ۺ��⡢������ͼ������ʣ����������ε��ж������ʣ�ƽ���ı��ε��ж������ʣ�����ϵ�����Լ������������֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬�����п�ѹ���⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
 �����������˵��������д���ݣ�
�����������˵��������д���ݣ�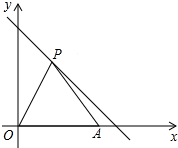 ��ͼ����A����Ϊ��4��0������P�ڵ�һ��������ֱ��y=-x+5�ϣ�
��ͼ����A����Ϊ��4��0������P�ڵ�һ��������ֱ��y=-x+5�ϣ�