题目内容
 如图,菱形ABCD的边长为8cm,∠BAD=120°,半径为
如图,菱形ABCD的边长为8cm,∠BAD=120°,半径为| 3 |
考点:轨迹
专题:
分析:求得当⊙O和∠B的两边相切到与∠C的两边相切时,两种情况下两个切点之间的距离,即圆心移动的距离,则滚动一周的路程即可求解.
解答: 解:当圆在⊙O的位置是,连接OB,连接O和切点E.
解:当圆在⊙O的位置是,连接OB,连接O和切点E.
∵菱形ABCD中,∠BAD=120°,
∴∠ABC=60°,
∴∠OBE=30°,
∴BE=
=
=3(cm);
当⊙O在⊙O'时,∠O'CF=60°,
则CF=
=
=1(cm),
则EF=8-3-1=4(cm),
则当⊙O第一次回到起始位置时,圆心O所走过的路程长度为4×4=16(cm).
故答案是:16.
 解:当圆在⊙O的位置是,连接OB,连接O和切点E.
解:当圆在⊙O的位置是,连接OB,连接O和切点E.∵菱形ABCD中,∠BAD=120°,
∴∠ABC=60°,
∴∠OBE=30°,
∴BE=
| OE |
| tan∠OBE |
| ||||
|
当⊙O在⊙O'时,∠O'CF=60°,
则CF=
| O′F |
| tan∠O′CF |
| ||
| tan60° |
则EF=8-3-1=4(cm),
则当⊙O第一次回到起始位置时,圆心O所走过的路程长度为4×4=16(cm).
故答案是:16.
点评:本题考查切线长定理以及三角函数,正确求得BE和CF的长度是关键.

练习册系列答案
相关题目
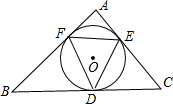 如图,△ABC的内切圆⊙O与各边相切于点D、E、F,且∠FOD=∠EOD=135°,则△ABC一定不是( )
如图,△ABC的内切圆⊙O与各边相切于点D、E、F,且∠FOD=∠EOD=135°,则△ABC一定不是( )| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
 甲乙两车分别从A、B两地同时出发相向而行.乙车出发1小时后出现故障,停下来维修半小时后继续前行.甲乙两车距A地的路程y1(千米)、y2(千米)与出发时间x(时)之间的函数图象如图所示:
甲乙两车分别从A、B两地同时出发相向而行.乙车出发1小时后出现故障,停下来维修半小时后继续前行.甲乙两车距A地的路程y1(千米)、y2(千米)与出发时间x(时)之间的函数图象如图所示: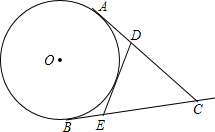 AC,BC是⊙O的两条过点C的切线,D,E分别是AC,BC边上的一点,如果△CED周长为AC的2倍,问DE与⊙O的位置关系.
AC,BC是⊙O的两条过点C的切线,D,E分别是AC,BC边上的一点,如果△CED周长为AC的2倍,问DE与⊙O的位置关系. 如图所示,已知PA=PB,∠1+∠2=180°.求证:OP平分∠AOB.
如图所示,已知PA=PB,∠1+∠2=180°.求证:OP平分∠AOB. 如图,在△ABD和△ACE中,∠BAD=∠CAE=90°,AD=AE,AC=AE.
如图,在△ABD和△ACE中,∠BAD=∠CAE=90°,AD=AE,AC=AE.