题目内容
 甲乙两车分别从A、B两地同时出发相向而行.乙车出发1小时后出现故障,停下来维修半小时后继续前行.甲乙两车距A地的路程y1(千米)、y2(千米)与出发时间x(时)之间的函数图象如图所示:
甲乙两车分别从A、B两地同时出发相向而行.乙车出发1小时后出现故障,停下来维修半小时后继续前行.甲乙两车距A地的路程y1(千米)、y2(千米)与出发时间x(时)之间的函数图象如图所示:(1)求甲车的速度;
(2)求乙车维修后距A地的路程y1与x之间的函数关系;
(3)出发多长时间时两车之间相距25千米?
考点:一次函数的应用
专题:
分析:(1)由函数图象数据,根据路程÷速度=时间就可以得出结论;
(2)设乙车维修后距A地的路程y1与x之间的函数关系为y1=k1x+b1,由待定系数法求出其解即可;
(3)先分别求出OA,BC的解析式,再根据解析式建立方程求出其解即可.
(2)设乙车维修后距A地的路程y1与x之间的函数关系为y1=k1x+b1,由待定系数法求出其解即可;
(3)先分别求出OA,BC的解析式,再根据解析式建立方程求出其解即可.
解答:解:(1)由题意,得
甲车的速度为:200÷2.5=80千米/时.
答:甲车的速度为80千米/时;
(2)设乙车维修后距A地的路程y1与x之间的函数关系为y1=k1x+b1,由题意,得
,
解得:
.,
∴乙车维修后距A地的路程y1与x之间的函数关系y=-70x+245(1.5≤x≤3.5);
(3)设直线OA,BC的解析式分别为y=kx,y2=k2x+b2,由题意,得
200=2.5k,
,
解得:k=80,
,
∴y=80x,y2=-60x+200(0≤x≤1).
CD的解析式为y3=140(1≤x≤1.5).
当y-y2=25时,80x-(-60x+200)=25,
解得:x=
>1(舍去),
当y3-y=25时,140-80x=25,
解得:x=
;
当y1-y=25时,-70x+245-80x=25,
x=
<1.5(舍去)
80x-140=25,
x=
>1.5(舍去),
但y-y1=25时,80x-(-70x+245)=25,
x=
.
综上所述:x=
,x=
时两车之间相距25千米.
甲车的速度为:200÷2.5=80千米/时.
答:甲车的速度为80千米/时;
(2)设乙车维修后距A地的路程y1与x之间的函数关系为y1=k1x+b1,由题意,得
|
解得:
|
∴乙车维修后距A地的路程y1与x之间的函数关系y=-70x+245(1.5≤x≤3.5);
(3)设直线OA,BC的解析式分别为y=kx,y2=k2x+b2,由题意,得

200=2.5k,
|
解得:k=80,
|
∴y=80x,y2=-60x+200(0≤x≤1).
CD的解析式为y3=140(1≤x≤1.5).
当y-y2=25时,80x-(-60x+200)=25,
解得:x=
| 45 |
| 28 |
当y3-y=25时,140-80x=25,
解得:x=
| 23 |
| 16 |
当y1-y=25时,-70x+245-80x=25,
x=
| 22 |
| 15 |
80x-140=25,
x=
| 33 |
| 16 |
但y-y1=25时,80x-(-70x+245)=25,
x=
| 9 |
| 5 |
综上所述:x=
| 23 |
| 16 |
| 9 |
| 5 |
点评:本题考查了一次函数的图象的性质的运用,行程问题的数量关系的运用,运用待定系数法求一次函数的解析式的运用,一元一次方程的解法的运用,解答时求出函数的解析式是关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
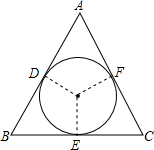 如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D、E、F.若∠ACB=90°,AB=AC=2,求圆的半径.
如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D、E、F.若∠ACB=90°,AB=AC=2,求圆的半径. 如图,菱形ABCD的边长为8cm,∠BAD=120°,半径为
如图,菱形ABCD的边长为8cm,∠BAD=120°,半径为 如图所示,AB=AD,BC=DC,E,F分别是DC、BC的中点,求证:AE=AF.
如图所示,AB=AD,BC=DC,E,F分别是DC、BC的中点,求证:AE=AF. 如图,△ABC中,AB=AC,E是AB上的任意一点,延长AC到F,连接EF交BC于M,且EM=FM,试说明线段BE与CF相等的理由.
如图,△ABC中,AB=AC,E是AB上的任意一点,延长AC到F,连接EF交BC于M,且EM=FM,试说明线段BE与CF相等的理由.