Question

7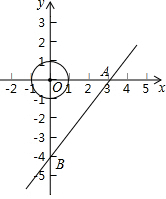．如图，在直角坐标系中，直线AB交x轴、y轴于点A（3，0）与B（0，-4），现有一半径为1的动圆的圆心位于原点处，动圆以每秒1个单位长度的速度向右作平移运动．设运动时间为t（秒），则动圆与直线AB相交时t的取值范围是$\frac{7}{4}$＜t＜$\frac{17}{4}$．

Answer 1

分析 在Rt△OAB中，OA=3，OB=4，由勾股定理得AB=5，过P点作AB的垂线，垂足为Q，PQ=1；当⊙O在直线AB的左边与直线AB相切时，AP=3-t，根据△APQ∽△ABO中的成比例线段求解；当⊙P在直线AB的右边与直线AB相切时，AP=t-3，根据△APQ∽△ABO中的成比例线段求解；得出动圆与直线AB相切时t的取值，即可得出动圆与直线AB相交时t的取值范围．

解答 解：如图所示：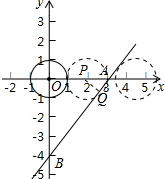
∵A（3，0）、B（0，-4），
∴OA=3，OB=4，
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5，
过P点作AB的垂线，垂足为Q，则PQ=1；
①当⊙P在直线AB的左边与直线AB相切时，AP=3-t，
则△APQ∽△ABO，
∴$\frac{AP}{AB}=\frac{PQ}{OB}$，即$\frac{3-t}{5}=\frac{1}{4}$，
解得：t=$\frac{7}{4}$；
②当⊙P在直线AB的右边与直线AB相切时，AP=t-3；
则△APQ∽△ABO，
∴$\frac{AP}{AB}=\frac{PQ}{OB}$，即$\frac{t-3}{5}=\frac{1}{4}$，
解得：t=$\frac{17}{4}$；
综上所述：动圆与直线AB相切时t的取值是$\frac{7}{4}$或$\frac{17}{4}$，
∴动圆与直线AB相交时t的取值范围是$\frac{7}{4}$＜t＜$\frac{17}{4}$．
故答案为：$\frac{7}{4}$＜t＜$\frac{17}{4}$．

点评 本题考查了圆的切线性质，及解直角三角形的知识．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．