题目内容
12.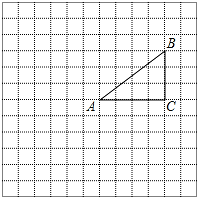 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.(1)在正方形网格中,画出△AB′C′;
(2)求出点B经过的路线长度;
(3)计算线段AC在变换到AC′的过程中扫过区域的面积.
分析 (1)利用网格特点和旋转的性质画出点B、C的对应点B′、C′,从而可得到△AB′C′;
(2)点B经过的路线为以点A为圆心,AB为半径,圆心角为90°的弧,然后根据弧长公式求解即可;
(3)线段AC在变换到AC′的过程中扫过区域为以A为圆心,AC为半径,圆心角为90°的扇形,然后根据扇形面积公式求解.
解答 解:(1)如图,△AB′C′为所作;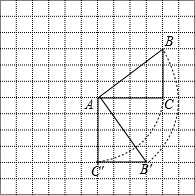
(2)AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
所以点B经过的路线长度=$\frac{90•π•5}{180}$=$\frac{5}{2}$π;
(3)线段AC在变换到AC′的过程中扫过区域的面积=$\frac{90π•{4}^{2}}{360}$=4π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了弧长公式和扇形面积公式.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 如图,在?ABCD中,E为CD上一点,连接AE,BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=2:3.
如图,在?ABCD中,E为CD上一点,连接AE,BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=2:3. 如图,在半⊙O中,P为直径AB上的一个动点,点C,D为半圆的三等分点,若AB=12,则图中阴影部分的面积为6π.
如图,在半⊙O中,P为直径AB上的一个动点,点C,D为半圆的三等分点,若AB=12,则图中阴影部分的面积为6π. 在同一直角坐标系中,一次函数y1=k1x+b与正比例函数y2=k2x的图象如图所示,则满足y1≥y2的x取值范围是x≤-2.
在同一直角坐标系中,一次函数y1=k1x+b与正比例函数y2=k2x的图象如图所示,则满足y1≥y2的x取值范围是x≤-2.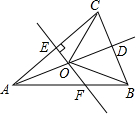 如图,在△ABC中,AB=AC,点D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F.
如图,在△ABC中,AB=AC,点D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F.