题目内容
2.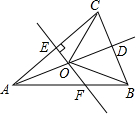 如图,在△ABC中,AB=AC,点D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F.
如图,在△ABC中,AB=AC,点D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F.(1)求证:点O在AB的垂直平分线上;
(2)若∠CAD=20°,求∠BOF的度数.
分析 (1)根据等腰三角形的性质可得AD⊥BC,根据垂直平分线的性质可得BO=AO,依此即可证明点O在AB的垂直平分线上;
(2)根据等腰三角形的性质可得∠BAD=∠CAD=20°,∠CAB=40°,再根据垂直的定义,等腰三角形的性质和角的和差故选即可得到∠BOF的度数.
解答 (1)证明:∵AB=AC,点D是BC的中点,
∴AD⊥BC,
∵AD是BC的垂直平分线,
∴BO=CO,
∵OE是AC的垂直平分线,
∴AO=CO,
∴BO=AO,
∴点O在AB的垂直平分线上;
(2)解:∵AB=AC,点D是BC的中点,
∴AD平分∠BAC,
∵∠CAD=20°,
∴∠BAD=∠CAD=20°,∠CAB=40°,
∵OE⊥AC,
∴∠EFA=90°-40°=50°,
∵AO=CO,
∴∠OBA=∠BAD=20°,
∴∠BOF=∠EFA-∠OBA=50°-20°=30°.
点评 考查了等腰三角形的性质,线段垂直平分线的性质,关键是熟练掌握等腰三角形三线合一的性质.

练习册系列答案
相关题目
10.已知一次函数y=(m-1)x+5-2m,若m的取值范围是1<m<$\frac{5}{2}$,则这个函数的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14. 如图,将边长为3cm的等边△ABC沿着边BC向右平移2cm,得到△DEF,则四边形ABFD的周长为( )
如图,将边长为3cm的等边△ABC沿着边BC向右平移2cm,得到△DEF,则四边形ABFD的周长为( )
 如图,将边长为3cm的等边△ABC沿着边BC向右平移2cm,得到△DEF,则四边形ABFD的周长为( )
如图,将边长为3cm的等边△ABC沿着边BC向右平移2cm,得到△DEF,则四边形ABFD的周长为( )| A. | 15cm | B. | 14cm | C. | 13cm | D. | 12cm |
11.在平面直角坐标系中,点P(-2015,2016)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
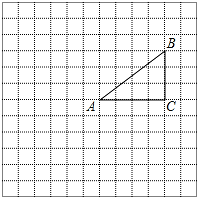 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′. 直角三角形的一个角是60°,用四个这样的直角三角形拼成如图所示的正方形ABCD,若正方形EFGH的边长是$\sqrt{3}$-1,则正方形ABCD的边长是2.
直角三角形的一个角是60°,用四个这样的直角三角形拼成如图所示的正方形ABCD,若正方形EFGH的边长是$\sqrt{3}$-1,则正方形ABCD的边长是2. 如图,点A在函数y=$\frac{2}{x}$(x>0)的图象上,点B在函数y=$\frac{6}{x}$(x>0)的图象上,点C在x轴上.若AB∥x轴,则△ABC的面积为2.
如图,点A在函数y=$\frac{2}{x}$(x>0)的图象上,点B在函数y=$\frac{6}{x}$(x>0)的图象上,点C在x轴上.若AB∥x轴,则△ABC的面积为2.