题目内容
18．
如图，在?ABCD中，E为CD上一点，连接AE，BD交于点F，S△DEF：S△ABF=4：25，则DE：EC=2：3．
分析 由四边形ABCD为平行四边形，得到对边平行且相等，利用两直线平行得到两对内错角相等，进而得到三角形DEF与三角形ABF相似，由相似三角形面积之比等于相似比的平方求出相似比，即可求出所求之比．
解答 解：∵四边形ABCD为平行四边形，
∴DC∥AB，DC=AB，
∴∠EDF=∠FBA，∠DEF=∠FAB，
∴△DEF∽△BAF，
∴S△DEF：S△ABF=（DE）2：（AB）2=4：25，
即DE：AB=2：5，
∴DE：DC=2：5，
则DE：EC=2：3，
故答案为：2：3
点评 此题考查了相似三角形的判定与性质，以及平行四边形的性质，熟练掌握相似三角形的判定与性质是解本题的关键．
练习册系列答案
相关题目
8．如果收入50元记作+50元，那么支出10元记作（ ）
| A． | +10元 | B． | -10元 | C． | +50元 | D． | -50元 |
如图，已知一次函数y=ax+b和y=kx的图象相交于点P，则根据图中信息可得二元一次方程组$\left\{\begin{array}{l}{y=ax+b}\\{kx-y=0}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$．
3．
小张从A地前往B地，到达后立刻返回．他与A地的距离y（千米）和所用的时间x（小时）之间的函数关系如图所示，则下列结论中错误的是（ ）
小张从A地前往B地，到达后立刻返回．他与A地的距离y（千米）和所用的时间x（小时）之间的函数关系如图所示，则下列结论中错误的是（ ）| A． | A、B两地的路程是240千米 | B． | 小张去时速度为80千米/小时 | ||
| C． | 小张从B地返回A地用了4小时 | D． | 小张返回时速度为80千米/小时 |
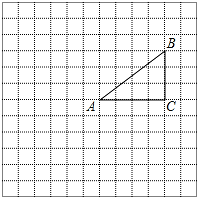如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△ABC的三个顶点A，B，C都在格点上，将△ABC绕点A按顺时针方向旋转90°得到△AB′C′．