题目内容
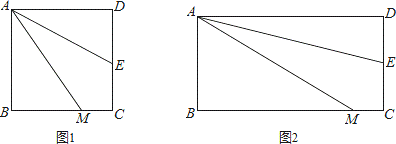
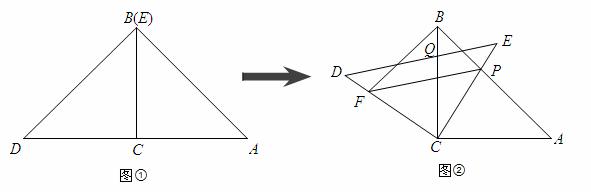
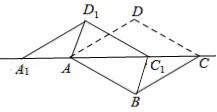
将两块全等的三角板如图①摆放,其中∠ACB=∠DCE=90°,∠A=∠D=45°,将图①中的△DCE顺时针旋转得图② ,点P是AB与CE的交点,点Q是DE
,点P是AB与CE的交点,点Q是DE 与BC的交点,在DC上取
与BC的交点,在DC上取 一点F,连接BE、FP,设BC=1,当BF⊥AB时,求△PBF面积的最大值。
一点F,连接BE、FP,设BC=1,当BF⊥AB时,求△PBF面积的最大值。
 解:∵∠ACB =90°,
解:∵∠ACB =90°, ∠A=45°,
∠A=45°,
∴∠A=∠ABC=45°。
∴AC=BC=1 。
∵BF⊥AB,
∴∠CBF=45°。
∴∠A=∠CBF。
由旋转的性质可得:∠BCF=∠ACP,
∴△BCF ≌△ACP(ASA)。
≌△ACP(ASA)。
∴BF=AP。
 ∵∠ACB =90°,∠A=45°,AC =1,
∵∠ACB =90°,∠A=45°,AC =1,
∴AB= 。
。
设BP=x ,则BF=AP
,则BF=AP =
= ,
,
∴ 。
。
∵ ,∴当x=
,∴当x=  时,S
时,S (ma
(ma x
x )=
)=  。
。
【考点】旋转问题,全等三角形的判定和 性质,旋转的性质,锐角三角函数定义,特殊角的
性质,旋转的性质,锐角三角函数定义,特殊角的 三角函数值,由实际问题列函数关系式,二次函数最值。
三角函数值,由实际问题列函数关系式,二次函数最值。


练习册系列答案
相关题目
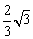 ;
; (0<x<
(0<x<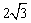 )。
)。


 动,线段PQ的垂直平分线为l:
动,线段PQ的垂直平分线为l: :如图一,抛物线
:如图一,抛物线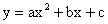
 与x轴正半轴交于A、B两点,与y轴交于点C,直线
与x轴正半轴交于A、B两点,与y轴交于点C,直线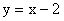
 经过A、C两点,且AB=2.
经过A、C两点,且AB=2.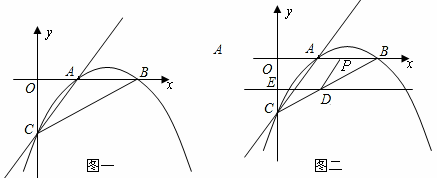

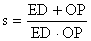
 ,当t 为何值时,s有最小值,并求出最小值。
,当t 为何值时,s有最小值,并求出最小值。 的图象经过点A、
的图象经过点A、 B和点C.连接AC,有两动点P、Q同时从点O出发,其中点P以每秒3个单位长度的速度沿折线OAC按O→A→C的路线运动,点Q以每秒8个单位长度的速度沿折线OCA按O→C→A的路线运动,当P、Q两点相遇时,它们都停止运动,设P、Q同时从点O出发t秒时,△OPQ的面
B和点C.连接AC,有两动点P、Q同时从点O出发,其中点P以每秒3个单位长度的速度沿折线OAC按O→A→C的路线运动,点Q以每秒8个单位长度的速度沿折线OCA按O→C→A的路线运动,当P、Q两点相遇时,它们都停止运动,设P、Q同时从点O出发t秒时,△OPQ的面 积为S.
积为S. 并写出自变量t的取值范围;
并写出自变量t的取值范围;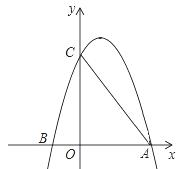
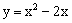 经过点A,B及原点O,顶点为C,直线OB为
经过点A,B及原点O,顶点为C,直线OB为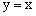 ,点P是抛物线上的动点,过点P作PM⊥x轴,
,点P是抛物线上的动点,过点P作PM⊥x轴, 垂足为M,是否存在点P,使得以P,M,A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
垂足为M,是否存在点P,使得以P,M,A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.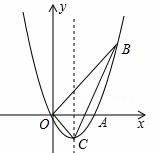
 .
.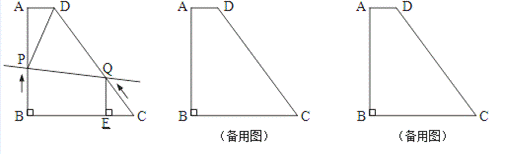

 C→D→A方向向点A运动;过点Q作QE
C→D→A方向向点A运动;过点Q作QE ?若存在,请求出t的值
?若存在,请求出t的值 从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从
从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从 度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ. 点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t
度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ. 点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t ≥0).
≥0).

 说明理由.
说明理由.