题目内容
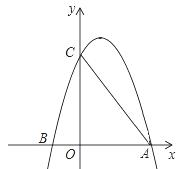
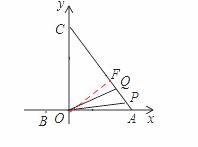
如图,已知二次函数 的图象经过点A、
的图象经过点A、 B和点C.连接AC,有两动点P、Q同时从点O出发,其中点P以每秒3个单位长度的速度沿折线OAC按O→A→C的路线运动,点Q以每秒8个单位长度的速度沿折线OCA按O→C→A的路线运动,当P、Q两点相遇时,它们都停止运动,设P、Q同时从点O出发t秒时,△OPQ的面
B和点C.连接AC,有两动点P、Q同时从点O出发,其中点P以每秒3个单位长度的速度沿折线OAC按O→A→C的路线运动,点Q以每秒8个单位长度的速度沿折线OCA按O→C→A的路线运动,当P、Q两点相遇时,它们都停止运动,设P、Q同时从点O出发t秒时,△OPQ的面 积为S.
积为S.
(1)请求出S关于t的函数关系式, 并写出自变量t的取值范围;
并写出自变量t的取值范围;
(2)设S0是②中函数S的 最大值,求出S0的值.
最大值,求出S0的值.
解:(1)∵二次函数的图象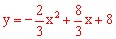 经过点A、B和点C,
经过点A、B和点C,
∴令y=0,得x=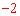 或x=6;令x=0,得y=8。
或x=6;令x=0,得y=8。
∴A(6,0),C(0,8)。
分三种情况讨论如下,

情况1:当0≤t≤1时,如图1,
S=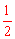 OP•OQ=
OP•OQ=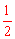 ×3t×8t=12t2。
×3t×8t=12t2。
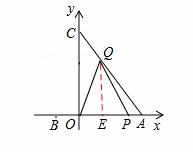
情况2:当1<t≤2时,如图2,
作QE⊥OA,垂足为E,
S=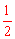 OP•EQ=
OP•EQ=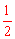 ×3t×
×3t×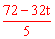
 。
。

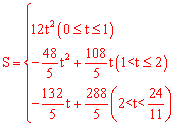 。
。
(2)根据(1)的函数即可得出S的最大值:
当0≤t≤1时,S =12t2,函数的最大值是12;
=12t2,函数的最大值是12;
当1<t≤2时,S ,函数的最大值是
,函数的最大值是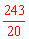 ;
;
当2<t<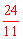
 ,S=
,S=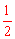 QP•OF
QP•OF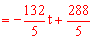 ,函数的最大值不超过
,函数的最大值不超过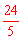
 。
。
∴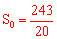 。
。
【考点】二次函数综合题,单双动点问题,曲线上点的坐标与方程 的关
的关 系,由实际问题列函数关系
系,由实际问题列函数关系 式,一次函数和二次函数的性质,分类思想、数形结合思想的应用。
式,一次函数和二次函数的性质,分类思想、数形结合思想的应用。


练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 ),且与y轴交于点C(0,
),且与y轴交于点C(0, ),与x轴交于A,B两点(点A在点B的左边)。
),与x轴交于A,B两点(点A在点B的左边)。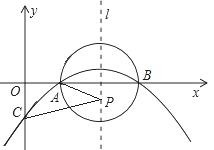
 ,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y,则当y=
,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y,则当y= 时,x的取
时,x的取 值是【 】
值是【 】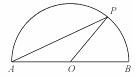
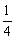 C. 1或
C. 1或 D.
D.  中,
中,

 .将
.将 绕点
绕点 按顺时针方向旋转n度后得到
按顺时针方向旋转n度后得到 ,此时点
,此时点 在
在 边上,斜边
边上,斜边 交
交 边于点
边于点
 ,则n的大小和图中阴影部分的面积分别为【 】
,则n的大小和图中阴影部分的面积分别为【 】
 B.
B. C.
C. D.
D.

 C值最小时PB的长.
C值最小时PB的长. ,点P是AB与CE的交点,点Q是DE
,点P是AB与CE的交点,点Q是DE 与BC的交点,在DC上取
与BC的交点,在DC上取 一点F,连接BE、FP,设BC=1,当BF⊥AB时,求△PBF面积的最大值。
一点F,连接BE、FP,设BC=1,当BF⊥AB时,求△PBF面积的最大值。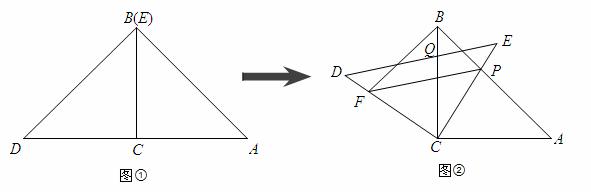
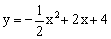 交y轴于点C
交y轴于点C ,对称轴与x轴交于点D,顶点为M,设点P(x,y)是第一象限内该抛物线上的一个动点,直线PE绕点P旋转,
,对称轴与x轴交于点D,顶点为M,设点P(x,y)是第一象限内该抛物线上的一个动点,直线PE绕点P旋转, 与y轴交于点E,是否存在以O、P、E为顶点的三角形与△OPD全等?若存在,请求出点E的坐标;若不存在,请说明理由。
与y轴交于点E,是否存在以O、P、E为顶点的三角形与△OPD全等?若存在,请求出点E的坐标;若不存在,请说明理由。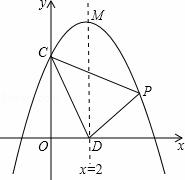

 ),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点
),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点 时,点Q也随之停止,设
时,点Q也随之停止,设 动的时间为t(秒).
动的时间为t(秒).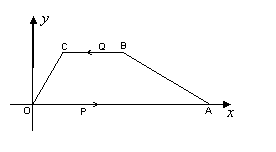

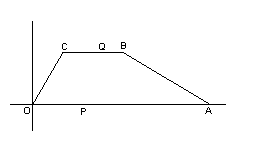

 (2)当点Q在CO边上运动时,求△OPQ的面积S与运动时间t的函数关系式,并写出自变量t的取值范围;
(2)当点Q在CO边上运动时,求△OPQ的面积S与运动时间t的函数关系式,并写出自变量t的取值范围; 的值;若不能,请说明理由.
的值;若不能,请说明理由.

 板,要求只剪2刀也拼成一个大正方形。
板,要求只剪2刀也拼成一个大正方形。