题目内容
如图,已知抛物线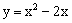 经过点A,B及原点O,顶点为C,直线OB为
经过点A,B及原点O,顶点为C,直线OB为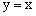 ,点P是抛物线上的动点,过点P作PM⊥x轴,
,点P是抛物线上的动点,过点P作PM⊥x轴, 垂足为M,是否存在点P,使得以P,M,A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
垂足为M,是否存在点P,使得以P,M,A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
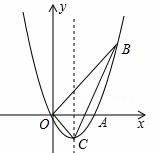
解:存在。

①若点P在第一象限,则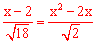 ,即
,即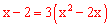 ,解得:x1=2,x2=
,解得:x1=2,x2=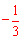 。
。
均不合题意。
②若点P在第二象限,则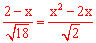 ,即
,即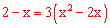 ,解得:x1=
,解得:x1=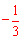 ,x2=2(不合题意,舍去)。
,x2=2(不合题意,舍去)。
当x=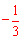 时,y=
时,y=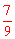 ,即P(
,即P(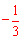 ,
,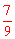 )。
)。
③若点P在第四象限,则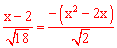 ,即
,即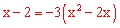 ,解得:x1=2,x2=
,解得:x1=2,x2=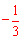 。均不合题意。
。均不合题意。
(2)若△PMA∽△BOC,则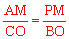 ,
,
①若点 P在第一象限,则
P在第一象限,则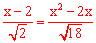 ,即
,即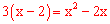 ,解得:x1=3,x2=2(不合题意,舍去)。
,解得:x1=3,x2=2(不合题意,舍去)。
当x=3时,y=3,即P(3,3)。
②若点P在第二象限,则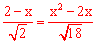 ,即
,即 ,解得:x1=
,解得:x1=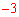 ,x2=2(不合题意
,x2=2(不合题意 ,舍去)。
,舍去)。
当x=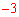 时,y=15,即P(
时,y=15,即P(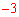 ,15)。
,15)。
③若点P在第四象限,则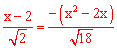 ,即
,即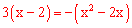 ,解得:x1=
,解得:x1=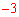 ,x2=2。均不合题意。
,x2=2。均不合题意。
综上所述,符合条件的点P有两个,分别是P(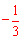 ,
,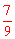 )或(3,3)或(
)或(3,3)或(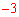 ,15)。
,15)。
【考点】二次函数综 合题,曲线上点的坐标与方程的关系,二次函数的性质,勾股定理和逆定理,相似三角形的性质,分类思想的应用。
合题,曲线上点的坐标与方程的关系,二次函数的性质,勾股定理和逆定理,相似三角形的性质,分类思想的应用。


练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目

 B.
B. C.
C. 8 D.
8 D.
 P垂直于AC的直
P垂直于AC的直

 D中,AH⊥DC,垂足为H,AB=
D中,AH⊥DC,垂足为H,AB=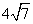 ,AD=7,AH=
,AD=7,AH=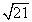 . 现有两个动点
. 现有两个动点 E、F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动. 在点E、F运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,当点E运
E、F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动. 在点E、F运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,当点E运 动到点C时,E、F两点同时停止运动. 设运转时间为t秒.
动到点C时,E、F两点同时停止运动. 设运转时间为t秒. 的面积为S,请直接写出S与t之间的函数关系式
的面积为S,请直接写出S与t之间的函数关系式 ,并写出相应的自变量t的取值范围;
,并写出相应的自变量t的取值范围; . 在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′. 设直线F′G′与射线DC、射
. 在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′. 设直线F′G′与射线DC、射 线AC分别相交于M、N两点.试问:是否存在点M、N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出线段CM的长度;若不存在,请说明理由.
线AC分别相交于M、N两点.试问:是否存在点M、N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出线段CM的长度;若不存在,请说明理由.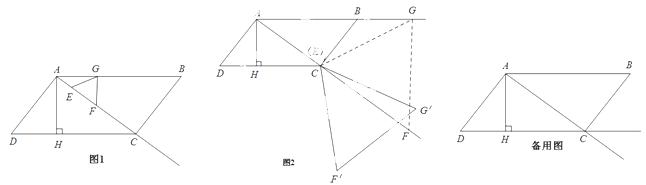
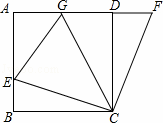
 ,点P是AB与CE的交点,点Q是DE
,点P是AB与CE的交点,点Q是DE 与BC的交点,在DC上取
与BC的交点,在DC上取 一点F,连接BE、FP,设BC=1,当BF⊥AB时,求△PBF面积的最大值。
一点F,连接BE、FP,设BC=1,当BF⊥AB时,求△PBF面积的最大值。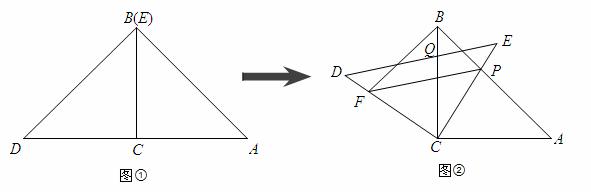
 从点A、B、C同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,
从点A、B、C同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时, 三个点随之停止移动.设移动开始后第ts时,△EFG的面积为Scm2。
三个点随之停止移动.设移动开始后第ts时,△EFG的面积为Scm2。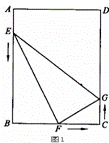



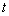
 =1s时,S的值是多少?
=1s时,S的值是多少?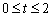
 时,点E、F、G分别在边AB、BC、CD上移动,用含
时,点E、F、G分别在边AB、BC、CD上移动,用含 t的代
t的代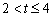
 与x轴交于点A,将线段OA绕点O逆时针旋转1200至OB的位置.
与x轴交于点A,将线段OA绕点O逆时针旋转1200至OB的位置. 的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.
的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.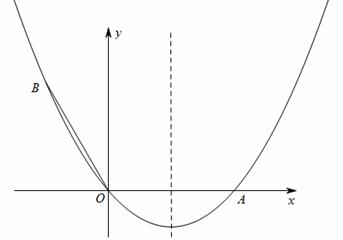
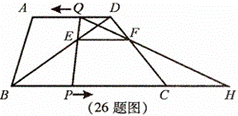
 别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm的速度沿DA向终点A移动,线段PQ与
别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm的速度沿DA向终点A移动,线段PQ与 BD相交于点E,过E作EF∥BC交CD于点F,射线QF交BC的延长线于点H,设动点P、Q移动的时间为t(单位:秒,0<t<10)。
BD相交于点E,过E作EF∥BC交CD于点F,射线QF交BC的延长线于点H,设动点P、Q移动的时间为t(单位:秒,0<t<10)。