题目内容
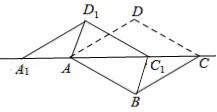
如图,将菱形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=2,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:
①△A1AD1≌△CC1B;
②当四边形ABC1D1是矩形时,x=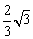 ;
;
③当x=2时,△BDD1为等腰直角三角形;
④ (0<x<
(0<x<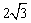 )。
)。
其中正确的是 (填序号)。
①②③④。
【考点】平移的性质,菱形的性质,全等三角形的判定,矩形的的判定,等腰直角三角形的判定,含30度直角三角形的性质。
【分析】①∵四边形ABCD为菱形,∴BC=AD,∠ACB =∠DAC。∴∠DAC=∠ACB。
∵把△ACD沿CA方向平移得到△A1C1D1,∴∠A1=∠DAC,A1D1=AD,AA1=CC1。
在△A1AD1与△CC1B中,∵AA1=CC1,∠A1=∠ACB,A1D1=CB,
∴△A1AD1≌△CC1B(SAS)。
故①正确。

②如图1,过点B作BH⊥AC于点H,
∵四边形ABC1D1是矩形,∠AC1D1=∠ACD=∠ACB=30°,
∴∠AC1B=60°。
∴∠C1BC=∠C1CB=30°。∴BC1= CC1=x。
∵AB=BC=2,∴B H=1,HC=
H=1,HC= 。
。
∴HC1= 。
。
∵HC=HC1+ CC1,∴ ,解得
,解得 。
。
故②正确。

③如图2,根据平移的性质,DD1=CC1=2,∠BDD1=90°,
根据菱形的性质和∠ACB=30°,可得DB=AB=2,
∴DD1= DB=2。
∴△BDD1为等腰直角三角 形。
形。
故③正确。



练习册系列答案
相关题目
 数
数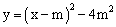
 (m>0)的图象与x轴交于A、B两点.
(m>0)的图象与x轴交于A、B两点.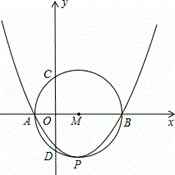

 B为直径的圆上,求二次函数的解析式;
B为直径的圆上,求二次函数的解析式;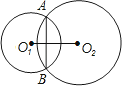
 B.10cm C.9cm D
B.10cm C.9cm D .8cm
.8cm 的长。
的长。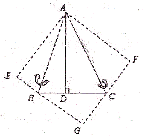

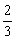 ),且与y轴交于点C(0,
),且与y轴交于点C(0,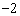 ),与x轴交于A,B两点(点A在点B的左边)。
),与x轴交于A,B两点(点A在点B的左边)。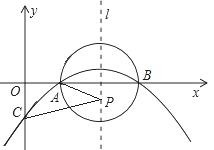

 B.
B. C.
C. 8 D.
8 D.
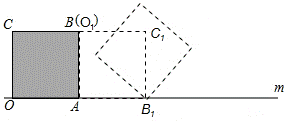

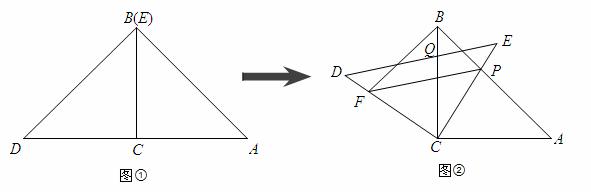
 ,点P是AB与CE的交点,点Q是DE
,点P是AB与CE的交点,点Q是DE 与BC的交点,在DC上取
与BC的交点,在DC上取 一点F,连接BE、FP,设BC=1,当BF⊥AB时,求△PBF面积的最大值。
一点F,连接BE、FP,设BC=1,当BF⊥AB时,求△PBF面积的最大值。