题目内容
已知 :如图一,抛物线
:如图一,抛物线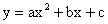
 与x轴正半轴交于A、B两点,与y轴交于点C,直线
与x轴正半轴交于A、B两点,与y轴交于点C,直线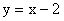
 经过A、C两点,且AB=2.
经过A、C两点,且AB=2.
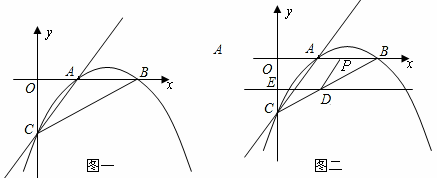

(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒 ;设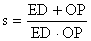
 ,当t 为何值时,s有最小值,并求出最小值。
,当t 为何值时,s有最小值,并求出最小值。
(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由。
(1)y=-1/4 x2+3/2 x-2(2)1(3)当t=2 /3 或t=10 / 7 时,以P、B、D为顶点的三角形与△ABC相似,证明见解析
/ 7 时,以P、B、D为顶点的三角形与△ABC相似,证明见解析
【解析】解:(1)由抛物线y=ax2+bx-2得:C(0,-2),
∴OA=OC=2,
∴A(2,0),
 ∵△ABC的面积为2,
∵△ABC的面积为2,
∴AB=2,
∴B(4,0),
∴设抛物线的解析式为y=a(x-2)(x-4),代入点C (0,-2),
(0,-2),
a=-1/4 ,
∴抛物线的解析式为y=-1/4 (x-2)(x-4)=-1/4 x2+3/2 x-2,
答 :抛物线的解析式为y=-1/4 x2+3/2 x-2.
:抛物线的解析式为y=-1/4 x2+3/2 x-2.
(2) 解:由题意:CE=t,PB
解:由题意:CE=t,PB =2t,OP=4-2t,
=2t,OP=4-2t,
∵ED∥BA
可得:ED /OB =CE /CO ,
即ED/4 =CE/2 ,
∴ED=2CE=2t,

②解:由题意可求:CD= 5 t,CB=2 5 ,
∴BD=2 5 - 5 t,
∵∠PBD=∠ABC,
∴以P、B、D为顶点的三角形与△ABC相似有两种情况:

(1)求出C的坐标,得到A、B的坐标,设抛物线的解析式为y=a (x-2)(x-4),代入点C的坐标求出a即可;
(x-2)(x-4),代入点C的坐标求出a即可;
(2)①由题意:CE= t,PB=2t,OP=4-2t,由ED∥BA得出EDOB =CE CO ,求出ED=2CE=2t,根据1 ED +1 OP =1 2t +1 4-2t =4 2t(4-2t) =1 -t2+2t ,求出即可;
t,PB=2t,OP=4-2t,由ED∥BA得出EDOB =CE CO ,求出ED=2CE=2t,根据1 ED +1 OP =1 2t +1 4-2t =4 2t(4-2t) =1 -t2+2t ,求出即可;
② 以P、B、D为顶点的三角形与△ABC相似有两种情况:BP AB =BD BC 和BP BD =
以P、B、D为顶点的三角形与△ABC相似有两种情况:BP AB =BD BC 和BP BD = BC BA 代入求出即可.
BC BA 代入求出即可.

 的长。
的长。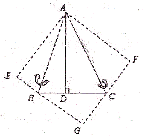

 P垂直于AC的直
P垂直于AC的直

 中,
中,

 .将
.将 绕点
绕点 按顺时针方向旋转n度后得到
按顺时针方向旋转n度后得到 ,此时点
,此时点 在
在 边上,斜边
边上,斜边 交
交 边于点
边于点
 ,则n的大小和图中阴影部分的面积分别为【 】
,则n的大小和图中阴影部分的面积分别为【 】
 B.
B. C.
C. D.
D.
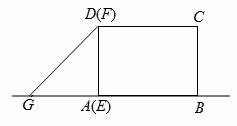
 D中,AH⊥DC,垂足为H,AB=
D中,AH⊥DC,垂足为H,AB=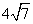 ,AD=7,AH=
,AD=7,AH=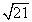 . 现有两个动点
. 现有两个动点 E、F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动. 在点E、F运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,当点E运
E、F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动. 在点E、F运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,当点E运 动到点C时,E、F两点同时停止运动. 设运转时间为t秒.
动到点C时,E、F两点同时停止运动. 设运转时间为t秒. 的面积为S,请直接写出S与t之间的函数关系式
的面积为S,请直接写出S与t之间的函数关系式 ,并写出相应的自变量t的取值范围;
,并写出相应的自变量t的取值范围; . 在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′. 设直线F′G′与射线DC、射
. 在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′. 设直线F′G′与射线DC、射 线AC分别相交于M、N两点.试问:是否存在点M、N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出线段CM的长度;若不存在,请说明理由.
线AC分别相交于M、N两点.试问:是否存在点M、N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出线段CM的长度;若不存在,请说明理由.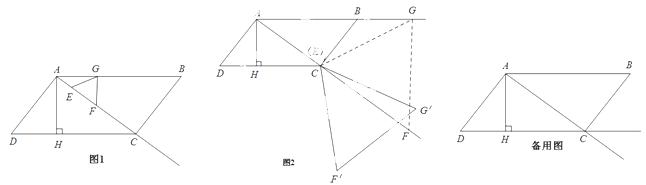
 ,点P是AB与CE的交点,点Q是DE
,点P是AB与CE的交点,点Q是DE 与BC的交点,在DC上取
与BC的交点,在DC上取 一点F,连接BE、FP,设BC=1,当BF⊥AB时,求△PBF面积的最大值。
一点F,连接BE、FP,设BC=1,当BF⊥AB时,求△PBF面积的最大值。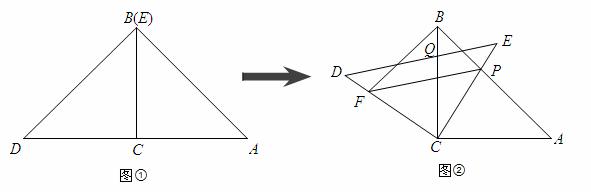
 与x轴交于点A,将线段OA绕点O逆时针旋转1200至OB的位置.
与x轴交于点A,将线段OA绕点O逆时针旋转1200至OB的位置. 的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.
的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.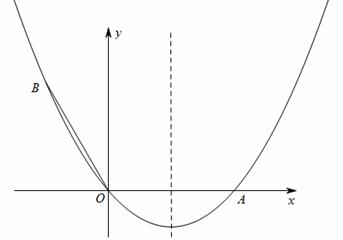
 点C匀速运动,速度为2cm/s;连接PQ。若设运动的时间为t(s)(0<t<2).根据以上信息,解答下列问题:
点C匀速运动,速度为2cm/s;连接PQ。若设运动的时间为t(s)(0<t<2).根据以上信息,解答下列问题: 积为y(
积为y(
 ),直接写出y与t之间的函数关系式;
),直接写出y与t之间的函数关系式; 如果将△APQ沿其一边所在直线翻折,翻折后的三角形与△APQ组成一个四边形,那么是否存在某一时刻t,使组成的四边形为菱形?若存在,求出t的值;若不存在,请说明理由.
如果将△APQ沿其一边所在直线翻折,翻折后的三角形与△APQ组成一个四边形,那么是否存在某一时刻t,使组成的四边形为菱形?若存在,求出t的值;若不存在,请说明理由.




