题目内容
如图,在矩形ABCD中,AB=3,BC=4.动点P从点A出发沿AC向终点C运动,同时动点Q从点B出发沿BA向点A运动,到达A点后立刻以原来的速度沿AB返回.点P、Q运动速度均为每秒1个单位长度,当点P到达点C时停止运动,点Q也同时停止.连接PQ,设运动时间为t(t >0)秒.


(1)求线段AC的长度;
(2)当点Q从点B向点A运动时(未到达A点),求△APQ的面积S关于t的函数关系式,并写出t的取值范围;
(3)伴随着P、Q两点的运 动,线段PQ的垂直平分线为l:
动,线段PQ的垂直平分线为l:
①当l经过点A时,射线QP交AD于点E,求AE的长;
②当l经过点B时,求t的值.
(1)5 (2)

 ,
, 
 (3)3、t=2.5,
(3)3、t=2.5,

【解析】
试题分析:(1)在矩形ABCD中,




(2)过点P作PH⊥AB于点H,AP=t,AQ =3-t,
由△AHP∽△A BC,得
BC,得
 ,∴PH=
,∴PH=
 ,
,

 ,
,

 .
.

②(ⅰ)如图③,当点Q从B向A运动时l经过 点B,
点B,


BQ=CP=AP=t,∠QBP=∠QAP
∵∠QBP+∠PBC=90°,∠QAP+∠PCB=90°
∴∠PBC=∠PCB CP=BP=AP=t
∴CP=AP=
 AC=
AC=
 ×5=2.5 ∴t=2.5.
×5=2.5 ∴t=2.5.
(ⅱ)如图④,当点Q从A向B运动时l经过点B,



考点:矩形、相似三角形
点评 :本题考查矩形,相似三
:本题考查矩形,相似三 角形,要求考生掌握矩形的性质,相似三角形的判定方法,会判定两个三角形相似
角形,要求考生掌握矩形的性质,相似三角形的判定方法,会判定两个三角形相似

练习册系列答案
相关题目
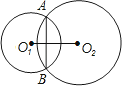
 B.10cm C.9cm D
B.10cm C.9cm D .8cm
.8cm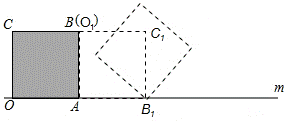

 ,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y,则当y=
,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y,则当y= 时,x的取
时,x的取 值是【 】
值是【 】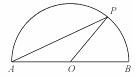
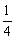 C. 1或
C. 1或 D.
D.  P垂直于AC的直
P垂直于AC的直

 中,
中,

 .将
.将 绕点
绕点 按顺时针方向旋转n度后得到
按顺时针方向旋转n度后得到 ,此时点
,此时点 在
在 边上,斜边
边上,斜边 交
交 边于点
边于点
 ,则n的大小和图中阴影部分的面积分别为【 】
,则n的大小和图中阴影部分的面积分别为【 】
 B.
B. C.
C. D.
D.
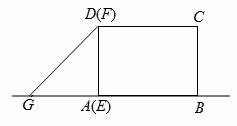
 ,点P是AB与CE的交点,点Q是DE
,点P是AB与CE的交点,点Q是DE 与BC的交点,在DC上取
与BC的交点,在DC上取 一点F,连接BE、FP,设BC=1,当BF⊥AB时,求△PBF面积的最大值。
一点F,连接BE、FP,设BC=1,当BF⊥AB时,求△PBF面积的最大值。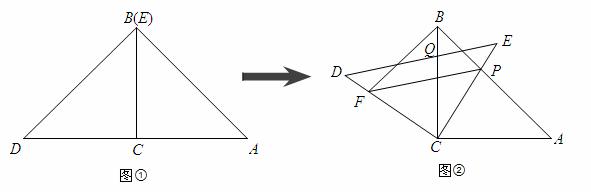
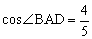 ,E是AB上一点,BE=2,AE=4BE,P是AC上一动点,则PB+PE的最小值是 .
,E是AB上一点,BE=2,AE=4BE,P是AC上一动点,则PB+PE的最小值是 .