题目内容
17. 已知:如图,AE是△ABC外角的平分线,且AE∥BC.
已知:如图,AE是△ABC外角的平分线,且AE∥BC.求证:△ABC是等腰三角形.
分析 由AE∥BC,根据平行线的性质,可求得∠DAE=∠B,∠EAC=∠C,又由AE是△ABC外角的平分线,即可得∠B=∠C,继而证得结论.
解答 证明:∵AE∥BC,
∴∠DAE=∠B,∠EAC=∠C,
∵AE是△ABC外角的平分线,
∴∠DAE=∠EAC,
∴∠B=∠C,
∴AB=AC,
即△ABC是等腰三角形.
点评 此题考查了等腰三角形的判定、平行线的性质以及角平分线的定义.注意等角对等边定理的应用是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.梯形上底为a,下底为b,高为(2a-b),则梯形的面积是( )
| A. | ${a^2}+\frac{1}{2}ab-\frac{1}{2}{b^2}$ | B. | 2a2+ab-b2 | C. | ${a^2}-\frac{1}{2}{b^2}$ | D. | ${a^2}+ab-\frac{1}{2}{b^2}$ |
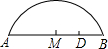
 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=20°,则∠C的度数是50°.
如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=20°,则∠C的度数是50°.
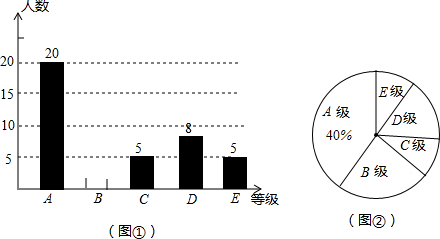
 如图,一拱桥呈抛物线状,桥的最大高度是32m,跨度是80m,在线段AB上距离中心M20m的D处,桥的高度是24m.
如图,一拱桥呈抛物线状,桥的最大高度是32m,跨度是80m,在线段AB上距离中心M20m的D处,桥的高度是24m.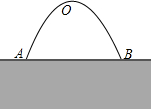 如图,桥拱是抛物线形,当水位线在AB位置时,水面宽为12m.此时水面与轿拱的最高点O距离是9米,当水面与桥拱的最高点O距离不小于4m,该桥可以安全通车,否则就必须要封闭桥面,问当桥拱内的水面宽在什么范围内,该轿可以安全通车?
如图,桥拱是抛物线形,当水位线在AB位置时,水面宽为12m.此时水面与轿拱的最高点O距离是9米,当水面与桥拱的最高点O距离不小于4m,该桥可以安全通车,否则就必须要封闭桥面,问当桥拱内的水面宽在什么范围内,该轿可以安全通车?