Question

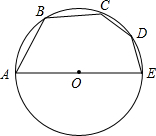如图，AE是⊙O的直径，弦AB=BC=4

2

，弦CD=DE=4，连接OB，OD，则⊙O的半径是（　　）

• A、4
• B、4

  2

• C、2

  10

• D、2

  2

  +2

Answer 1

考点：圆心角、弧、弦的关系,勾股定理,等腰直角三角形

专题：计算题

分析：连结BD、OC，作BH⊥CD于H，如图，根据圆心角、弧、弦的关系由AB=BC，CD=DE得到

AB

=

BC

，

CD

=

DE

，则∠1=∠AOB，∠2=∠DOE，所以∠1+∠2=

1

2

∠AOE=90°，则可判断△OBD为等腰直角三角形，得到BD=

2

OB，再根据圆周角定理得∠CBD=

1

2

∠2，∠BDC=

1

2

∠1，则∠CBD+∠BDC=45°，利用三角形外角性质得∠BCH=∠CBD+∠BDC=45°，得到△BCH为等腰直角三角形，可计算得BH=CH=

2

2

BC=4，DH=CD+HC=8，然后在Rt△BDH中理由勾股定理计算出BD=4

5

，于是有

2

OB=4

5

，再求出OB即可．

解答：解：连结BD、OC，作BH⊥CD于H，如图，
∵AB=BC，CD=DE，
∴

AB

=

BC

，

CD

=

DE

，
∴∠1=∠AOB，∠2=∠DOE，
∴∠1+∠2=

1

2

∠AOE=90°，
∴△OBD为等腰直角三角形，
∴BD=

2

OB，
∵∠CBD=

1

2

∠2，∠BDC=

1

2

∠1，
∴∠CBD+∠BDC=

1

2

（∠1+∠2）=45°，
∴∠BCH=∠CBD+∠BDC=45°，
∴△BCH为等腰直角三角形，
∴BH=CH=

2

2

BC=

2

2

•4

2

=4，
∴DH=CD+HC=4+4=8，
在Rt△BDH中，∵BH=4，DH=8，
∴BD=

BH2+DH2

=4

5

，
∴

2

OB=4

5

，
∴OB=2

10

．
故选C．

点评：本题考查了圆心角、弧、弦的关系：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等．也考查了圆周角定理和等腰直角三角形的判定与性质．