题目内容
11.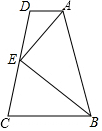 如图,在梯形ABCD中,AD∥BC,∠DAB和∠ABC的平分线交CD于同一点E,且E是CD的中点,求证:AB=AD+BC.
如图,在梯形ABCD中,AD∥BC,∠DAB和∠ABC的平分线交CD于同一点E,且E是CD的中点,求证:AB=AD+BC.
分析 在AB上截取AD=AD′,根据SAS证明△ADE≌△AD′E(SAS)和△CEB≌△D′EB(SAS),得到DE=ED′,BC=BD′,即可证明AB=BC+AD.
解答  证明:在AB上截取AD=AD′,
证明:在AB上截取AD=AD′,
∵∠DAB和∠ABC的平分线交CD于同一点E,且E是CD的中点,
∴∠DAE=∠EAB,∠ABE=∠EBC,DE=EC,
在△ADE和△AD′E中
$\left\{\begin{array}{l}{AD=AD′}\\{∠DAE=∠D′AE}\\{AE=AE}\end{array}\right.$,
∴△ADE≌△AD′E(SAS),
∴DE=ED′,∠DEA=∠D′EA,
又∵DE=EC,
∴EC=ED′,
∵AD∥BC,
∴∠DAE+∠CBE=∠EAB+∠ABE=90°,
∴∠AED′+∠BED′=∠DEA+∠CEB=90°,
又∵∠DEA=∠AED′,
∴∠CEB=∠BED′,
在△CEB和△D′EB中,
$\left\{\begin{array}{l}{ED′=EC}\\{∠D′EB=∠CEB}\\{EB=EB}\end{array}\right.$,
∴△CEB≌△D′EB(SAS),
∴BC=BD′,
∴AB=AD′+BD′=AD+BC.
点评 本题主要考查了全等三角形的判定与性质,在AB上截取AD=AD′,构造全等三角形是解决问题的关键.

练习册系列答案
相关题目
4.某地修一条公路,若甲工程队单独承包要80天完成,乙工程队单独承包要120天完成.现在由甲、乙工程队合作承包,完成任务需要( )
| A. | 48天 | B. | 60天 | C. | 80天 | D. | 100天 |
6.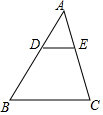 如图,在△ABC中,点D,E分别在线段AB,AC上,且DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,点D,E分别在线段AB,AC上,且DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$的值为( )
 如图,在△ABC中,点D,E分别在线段AB,AC上,且DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,点D,E分别在线段AB,AC上,且DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{2}$ |
19.对于任意实数x,点P(x,x2+4x+3)一定不在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
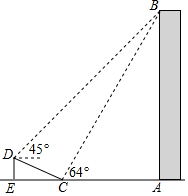 如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡度为1:$\frac{12}{5}$,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡度为1:$\frac{12}{5}$,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.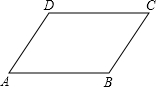 如图,AD∥BC,∠BAD=∠BCD,求证:AB∥CD.
如图,AD∥BC,∠BAD=∠BCD,求证:AB∥CD.