题目内容
2.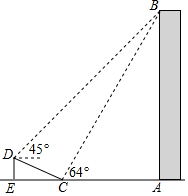 如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡度为1:$\frac{12}{5}$,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡度为1:$\frac{12}{5}$,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.(1)求斜坡CD的高度DE;
(2)求大楼AB的高度;(参考数据:sin64°≈0.9,tan64°≈2).
分析 (1)根据在大楼AB的正前方有一斜坡CD,CD=13米,坡度为1:$\frac{12}{5}$,高为DE,可以求得DE的高度;
(2)根据锐角三角函数和题目中的数据可以求得大楼AB的高度.
解答 解:(1)∵在大楼AB的正前方有一斜坡CD,CD=13米,坡度为1:$\frac{12}{5}$,
∴$\frac{DE}{EC}=\frac{1}{\frac{12}{5}}=\frac{5}{12}$,
设DE=5x米,则EC=12x米,
∴(5x)2+(12x)2=132,
解得,x=1,
∴5x=5,12x=12,
即DE=5米,EC=12米,
故斜坡CD的高度DE是5米;
(2)∵tan64°=$\frac{AB}{AC}$,tan45°=$\frac{AB-DE}{EC+AC}$,DE=5米,CE=12米,
∴2=$\frac{AB}{AC}$,1=$\frac{AB-5}{12+AC}$,
解得,AB=34米,AC=17米,
即大楼AB的高度是34米.
点评 本题考查解直角三角形的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用坡度和锐角三角函数解答问题.

练习册系列答案
相关题目
 如图,已知等边△ABC,在平面上找一点P,使得△PAB、△PBC和△PAC都是等腰三角形,这样的点P的个数是( )
如图,已知等边△ABC,在平面上找一点P,使得△PAB、△PBC和△PAC都是等腰三角形,这样的点P的个数是( )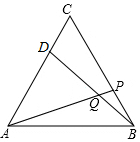 如图,在等边△ABC的顶点B、C处各有一只蜗牛,它们同时出发,分别都以每分钟1个单位的速度由C向A和由B向C爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t分钟后,它们分别爬行到D、P处,请问:
如图,在等边△ABC的顶点B、C处各有一只蜗牛,它们同时出发,分别都以每分钟1个单位的速度由C向A和由B向C爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t分钟后,它们分别爬行到D、P处,请问: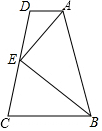 如图,在梯形ABCD中,AD∥BC,∠DAB和∠ABC的平分线交CD于同一点E,且E是CD的中点,求证:AB=AD+BC.
如图,在梯形ABCD中,AD∥BC,∠DAB和∠ABC的平分线交CD于同一点E,且E是CD的中点,求证:AB=AD+BC.