题目内容
17．已知多项式（x+3）（x+n）=x2+mx-21，则m的值是（ ）| A． | -4 | B． | 4 | C． | -2 | D． | 2 |
分析 将等式左边根据多项式乘多项式法则展开，将m看作常数合并同类项，利用多项式相等的条件得出关于m、n的方程组，解方程组求出m与n的值．
解答 解：（x+3）（x+n）=x2+mx-21，
x2+nx+3x+3n=x2+mx-21，
x2+（n+3）x+3n=x2+mx-21，
则$\left\{\begin{array}{l}{n+3=m}\\{3n=-21}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{m=-4}\\{n=-7}\end{array}\right.$．
故选：A．
点评 本题主要考查多项式乘多项式，根据多项式相等得出关于m、n的方程组是解题的关键．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
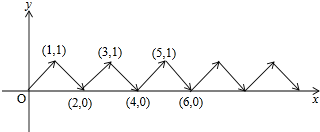如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，1），…，按这样的运动规律，经过第2016次运动后，点P运动的总长度是2016$\sqrt{2}$．
5．
如图，将矩形ABCD沿AE对折，使点D落在点F处，若∠CEF=60°，则∠EAF等于（ ）
如图，将矩形ABCD沿AE对折，使点D落在点F处，若∠CEF=60°，则∠EAF等于（ ）| A． | 60° | B． | 50° | C． | 40° | D． | 30° |
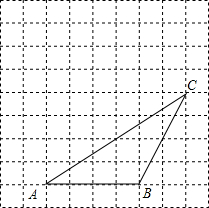如图，网格中每个小正方形边长为1，△ABC的顶点都在格点上．将△ABC向左平移2格，再向上平移3格，得到△A′B′C′．