题目内容
8.解方程组:$\left\{\begin{array}{l}{4x-3z=17}\\{3x+y+5z=18}\\{x+2y+z=2}\end{array}\right.$.分析 ②×2-③得出5x+9z=34④,由①和④组成一个二元一次方程组,求出方程组的解,把x=5,z=1代入③求出y即可.
解答 解:$\left\{\begin{array}{l}{4x-3z=17①}\\{3x+y+5z=18②}\\{x+2y+z=2③}\end{array}\right.$
②×2-③得:5x+9z=34④,
由①和④组成一个二元一次方程组:$\left\{\begin{array}{l}{4x-3z=17}\\{5x+9z=34}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=5}\\{z=1}\end{array}\right.$,
把x=5,z=1代入③得:5+2y+1=2,
解得:y=-2,
所以原方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=-2}\\{z=1}\end{array}\right.$.
点评 本题考查了解三元一次方程组的应用,解此题的关键是能正确消元,即把三元一次方程转化成二元一次方程组,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.“任意买一张电影票,座位号是2的倍数”,此事件是( )
| A. | 不可能事件 | B. | 随机事件 | C. | 必然事件 | D. | 确定事件 |
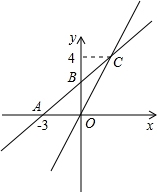 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=$\frac{4}{3}$x的图象交点为C(m,4).求:
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=$\frac{4}{3}$x的图象交点为C(m,4).求: 我们可以计算出
我们可以计算出