题目内容
已知两圆的圆心距d为4，两圆的半径R、r分别是方程x2-4x+3=0的两根，试确定两个圆的位置关系．
考点：圆与圆的位置关系,解一元二次方程-因式分解法
专题：
分析：先根据一元二次方程根与系数的关系，可知圆心距＞两圆半径之和，再根据圆与圆的位置关系即可判断．
解答：解：∵两圆的半径是方程x2-4x+3=0的两个根，
∴两根之和=4=两圆半径之和，
又∵圆心距=4，
∴两圆外切．
∴两根之和=4=两圆半径之和，
又∵圆心距=4，
∴两圆外切．
点评：此题综合考查一元二次方程根与系数的关系及两圆的位置关系的判断．
圆和圆的位置与两圆的圆心距、半径的数量之间的关系：
①两圆外离?d＞R+r；
②两圆外切?d=R+r；
③两圆相交?R-r＜d＜R+r（R≥r）；
④两圆内切?d=R-r（R＞r）；
⑤两圆内含?d＜R-r（R＞r）．
圆和圆的位置与两圆的圆心距、半径的数量之间的关系：
①两圆外离?d＞R+r；
②两圆外切?d=R+r；
③两圆相交?R-r＜d＜R+r（R≥r）；
④两圆内切?d=R-r（R＞r）；
⑤两圆内含?d＜R-r（R＞r）．
练习册系列答案
相关题目
使分式
的值等于零的条件是（ ）
| x+a |
| 2x-3 |
A、x=
| ||
| B、x=-a | ||
C、x=-a且a≠-
| ||
D、x=-a且a≠
|
如图，方格纸上的每个小方格都是边长为1 的正方形，△ABC的顶点均在格点上，若B点的坐标为（-4，-2）按要求回答下列问题
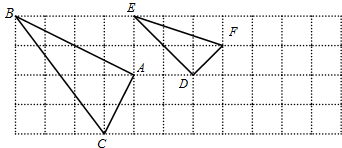
如图所示，轮船在A处观测到北偏东45°方向上有个灯塔B，轮船在正东方向20海里1.5小时后到达C处，又观测到灯塔B在北偏东30°方向上，则此时轮船与灯塔B相距海里．（结果保留根号）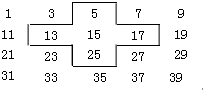
将连续的奇数1，3，5，7，9…排成如下的数表：