题目内容
如图,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在方格纸的格点上.
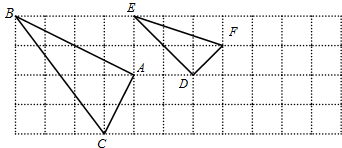
(1)判断△ABC和△DEF是否相似,并说明理由;
(2)以点E为中心,在位似中心的同侧画出△EDF的一个位似△ED1F1,使得它与△EDF的相似比为2:1;
(3)求△ABC与△ED1F1的面积比.

(1)判断△ABC和△DEF是否相似,并说明理由;
(2)以点E为中心,在位似中心的同侧画出△EDF的一个位似△ED1F1,使得它与△EDF的相似比为2:1;
(3)求△ABC与△ED1F1的面积比.
考点:作图-位似变换,相似三角形的判定与性质
专题:几何变换
分析:(1)先利用勾股定理计算出两个三角形的所有边长,通过计算对应边的比得到
=
=
,再根据相似三角形的判定方法即可得到△ABC∽△DEF;
(2)根据画位似图形的方法画出△ED1F1;
(3)易得△ABC∽△D1EF1,然后根据相似三角形面积的比等于相似比的平方进行计算.
| BC |
| EF |
| AC |
| FD |
| AB |
| ED |
(2)根据画位似图形的方法画出△ED1F1;
(3)易得△ABC∽△D1EF1,然后根据相似三角形面积的比等于相似比的平方进行计算.
解答:解:(1)∵AB=2
,AC=
,BC=5,EF=
,FD=
,ED=2
,
∴
=
=
,
=
=
,
=
=
,
∴
=
=
,
∴△ABC∽△DEF;
(2)延长ED到点D1,使ED1=2ED,延长EF到点F1,使EF1=2EF,连结D1F1,则△ED1F1为所求,如图;
(3)∵△ABC∽△DEF,△DEF∽△D1EF1,
∴△ABC∽△D1EF1,
∴△ABC与△ED1F1的面积比=(
)2=(
)2=
.
| 5 |
| 5 |
| 10 |
| 2 |
| 2 |
∴
| BC |
| EF |
| 5 | ||
|
| ||
| 2 |
| AC |
| FD |
| ||
|
| ||
| 2 |
| AB |
| ED |
2
| ||
2
|
| ||
| 2 |

∴
| BC |
| EF |
| AC |
| FD |
| AB |
| ED |
∴△ABC∽△DEF;
(2)延长ED到点D1,使ED1=2ED,延长EF到点F1,使EF1=2EF,连结D1F1,则△ED1F1为所求,如图;
(3)∵△ABC∽△DEF,△DEF∽△D1EF1,
∴△ABC∽△D1EF1,
∴△ABC与△ED1F1的面积比=(
| AC |
| D1F1 |
| ||
2
|
| 5 |
| 8 |
点评:本题考查了作图-位似变化:确定位似中心;分别连接并延长位似中心和能代表原图的关键点;根据位似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.也考查了相似三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果不等式组
无解,则a的取值范围是( )
|
| A、a<1 | B、a≤1 |
| C、a>1 | D、a≥1 |
 将1、
将1、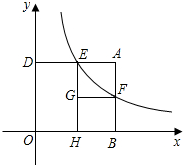 (1)阅读合作学习内容,解答其中的问题;
(1)阅读合作学习内容,解答其中的问题;  已知:如图,直角坐标系中线段AB的端点坐标分别是A(-2,2),B(2,3);在坐标系中画出线段AB关于x轴的对称图形线段A′B′;并写出两端点的坐标:点A′
已知:如图,直角坐标系中线段AB的端点坐标分别是A(-2,2),B(2,3);在坐标系中画出线段AB关于x轴的对称图形线段A′B′;并写出两端点的坐标:点A′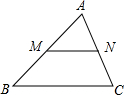 如图,在△ABC中,AB=7,AC=6,BC=8,点M是AB上的一个动点,MN∥BC交AC于点N,若点M从点B处开始向点A方向运动,速度为每秒2个单位.
如图,在△ABC中,AB=7,AC=6,BC=8,点M是AB上的一个动点,MN∥BC交AC于点N,若点M从点B处开始向点A方向运动,速度为每秒2个单位.