题目内容
 如图所示,轮船在A处观测到北偏东45°方向上有个灯塔B,轮船在正东方向20海里1.5小时后到达C处,又观测到灯塔B在北偏东30°方向上,则此时轮船与灯塔B相距海里.(结果保留根号)
如图所示,轮船在A处观测到北偏东45°方向上有个灯塔B,轮船在正东方向20海里1.5小时后到达C处,又观测到灯塔B在北偏东30°方向上,则此时轮船与灯塔B相距海里.(结果保留根号)考点:解直角三角形的应用-方向角问题
专题:
分析:作CD⊥AB于点D,则△ABD是等腰直角三角形,设CD=x,则AD=BD=20+x(m),在直角△BCD中,利用三角函数即可得到关于x的方程,从而求得x的值,进而利用三角函数求得BC的值.
解答: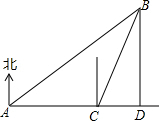 解:作BD⊥AC于点D.
解:作BD⊥AC于点D.
设CD=x,则AD=AC+CD=20+x(m),
∵直角△ABD中,∠BAD=45°,
∴BD=AD=20+x,
在直角△BCD中,∠BCD=80°-30°=60°,
tan∠BCD=
=
=tan60°=
,
则x=10(
+1),
则BC=2x=20(
+1)(海里).
答:此时轮船与灯塔B相距20(
+1)海里.
 解:作BD⊥AC于点D.
解:作BD⊥AC于点D.设CD=x,则AD=AC+CD=20+x(m),
∵直角△ABD中,∠BAD=45°,
∴BD=AD=20+x,
在直角△BCD中,∠BCD=80°-30°=60°,
tan∠BCD=
| BD |
| CD |
| 20+x |
| x |
| 3 |
则x=10(
| 3 |
则BC=2x=20(
| 3 |
答:此时轮船与灯塔B相距20(
| 3 |
点评:本题主要考查了方向角含义,解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
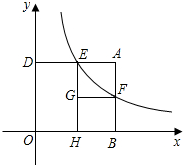 (1)阅读合作学习内容,解答其中的问题;
(1)阅读合作学习内容,解答其中的问题; 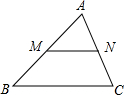 如图,在△ABC中,AB=7,AC=6,BC=8,点M是AB上的一个动点,MN∥BC交AC于点N,若点M从点B处开始向点A方向运动,速度为每秒2个单位.
如图,在△ABC中,AB=7,AC=6,BC=8,点M是AB上的一个动点,MN∥BC交AC于点N,若点M从点B处开始向点A方向运动,速度为每秒2个单位. 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AC和BD相交于点E,AC=BC,DE=2cm,AD=5cm,则⊙O的半径为是
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AC和BD相交于点E,AC=BC,DE=2cm,AD=5cm,则⊙O的半径为是
 已知:如图,在△ABC中,点E、F分别是AB、AC上的点,且EF∥BC,BM是线段CF的垂直平分线,垂足为M.N是线段BM上一点,且NC=EF.
已知:如图,在△ABC中,点E、F分别是AB、AC上的点,且EF∥BC,BM是线段CF的垂直平分线,垂足为M.N是线段BM上一点,且NC=EF.