题目内容
4.某玩具店用2000元购进一批玩具,面市后,供不应求,于是店主又购进同样的玩具,所购的数量是第一批数量的3倍,但每件进价贵了4元,结果购进第二批玩具共用了6300元.若两批玩具的售价都是每件120元,且两批玩具全部售完.(1)第一次购进了多少件玩具?
(2)求该玩具店销售这两批玩具共盈利多少元?
分析 (1)设第一次购进了x件玩具,则第二购进了3x件玩具,根据单价=总价÷数量结合第二批的进价比第一批每件贵了4元即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)根据利润=销售收入-成本即可算出该玩具店销售这两批玩具共盈利多少元.
解答 解:(1)设第一次购进了x件玩具,则第二购进了3x件玩具,
根据题意得:$\frac{6300}{3x}$-$\frac{2000}{x}$=4,
解得:x=25,
经检验,x=25是原分式方程的解.
答:第一次购进了25件玩具.
(2)(25+25×3)×120-2000-6300=3700(元).
答:该玩具店销售这两批玩具共盈利3700元.
点评 本题考查了分式方程的应用,解题的关键是:(1)根据单价=总价÷数量结合第二批的进价比第一批每件贵了4元列出关于x的分式方程;(2)根据利润=销售收入-成本列式计算.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
14.下列命题中,真命题是( )
| A. | 底边对应相等的两个等腰三角形全等 | |
| B. | 腰对应相等的两个等腰三角形全等 | |
| C. | 斜边对应相等的两个直角三角形全等 | |
| D. | 面积相等的两个等边三角形全等 |
15.某区今年暑假选派了180名教师担任G20交通引导志愿者、80名教师担任安全维护志愿者,现要把一部分安全维护志愿者调到交通引导志愿者队伍中,使安全维护志愿者人数占交通引导志愿者人数的30%,设把x名安全维护志愿者调到交通引导志愿者队伍中,则可列方程( )
| A. | 80-x=30%×(180+x) | B. | 80-x=30%×180 | C. | 180+x=30%×(80-x) | D. | 80-x=30%×260 |
19.无论x、y取任何值,多项式x2+y2-2x-4y+6的值总是( )
| A. | 正数 | B. | 负数 | C. | 非负数 | D. | 无法确定 |
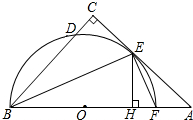 如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.

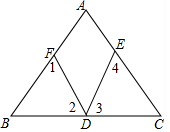 如图,D为BC上一点,∠1=∠2,∠3=∠4,∠A=50°,求∠EDF的度数.
如图,D为BC上一点,∠1=∠2,∠3=∠4,∠A=50°,求∠EDF的度数.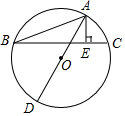 如图,A,B,C为⊙O上的点,AD为⊙O的直径,AE⊥BC于E,AB=5,BE=$\sqrt{21}$,CE=$\sqrt{5}$,求AD的长.
如图,A,B,C为⊙O上的点,AD为⊙O的直径,AE⊥BC于E,AB=5,BE=$\sqrt{21}$,CE=$\sqrt{5}$,求AD的长.