题目内容
20.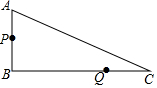 如图,在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm.点P从点A沿AB方向以1cm/s的速度运动至点B,点Q从点B沿BC方向以6cm/s的速度运动至点C,P、Q两点同时出发.
如图,在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm.点P从点A沿AB方向以1cm/s的速度运动至点B,点Q从点B沿BC方向以6cm/s的速度运动至点C,P、Q两点同时出发.(1)求BC的长.
(2)若运动2s时,求P、Q两点之间的距离.
(3)P、Q两点运动几秒,AP=CQ.
分析 (1)在直角△ABC中,根据勾股定理来求BC的长度;
(2)在直角△BPQ中,根据勾股定理来求PQ的长度;
(3)由路程=时间×速度求出AP,BQ,再根据等量关系:AP=CQ列出方程求解即可.
解答 解:(1)∵在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=24cm.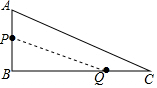 (2)如图,连结PQ,
(2)如图,连结PQ,
BP=7-2=5,
BQ=6×2=12,
在直角△BPQ中,由勾股定理得到:PQ=$\sqrt{B{P}^{2}+B{Q}^{2}}$=13(cm);
(3)设t秒后,AP=CQ.则
t=24-6t,
解得 t=$\frac{24}{7}$.
答:P、Q两点运动$\frac{24}{7}$秒,AP=CQ.
点评 本题考查了勾股定理和一元一次方程的定义.解题时,需要熟悉路程=时间×速度,以及变形后的公式.

练习册系列答案
相关题目
12.下列说法正确的是( )
| A. | 2πx2的系数是2 | B. | -xy2的次数为2 | C. | -5x2+x=-4x3 | D. | 3x2-x2=2x2 |
9.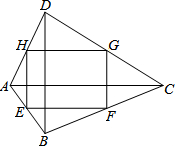 如图,四边形ABCD中,AC=8,BD=6,且AC⊥BD,连接四边形ABCD各边中点得到四边形EFGH,下列说法正确的是( )
如图,四边形ABCD中,AC=8,BD=6,且AC⊥BD,连接四边形ABCD各边中点得到四边形EFGH,下列说法正确的是( )
 如图,四边形ABCD中,AC=8,BD=6,且AC⊥BD,连接四边形ABCD各边中点得到四边形EFGH,下列说法正确的是( )
如图,四边形ABCD中,AC=8,BD=6,且AC⊥BD,连接四边形ABCD各边中点得到四边形EFGH,下列说法正确的是( )| A. | 四边形EFGH是矩形 | B. | 四边形EFGH的周长是7 | ||
| C. | 四边形EFGH的面积是24 | D. | 四边形ABCD的面积是48 |
8.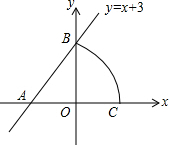 如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为( )
如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为( )
 如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为( )
如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为( )| A. | (3$\sqrt{2}$-3,0) | B. | (3$\sqrt{2}$,0) | C. | (0,3$\sqrt{2}$-3) | D. | (3,0) |
 如图,⊙O的半径为1,点A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,⊙O的半径为1,点A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.