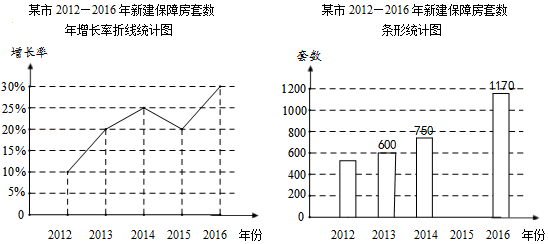
题目内容
19.【问题探究】已知:如图①所示,∠MPN的顶点为P,⊙O的圆心O从顶点P出发,沿着PN方向平移.
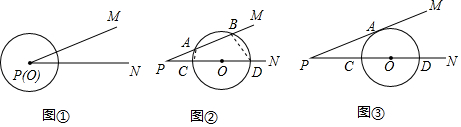
(1)如图②所示,当⊙O分别与射线PM,PN相交于A、B、C、D四个点,连接AC、BD,可以证得△PAC∽△△PDB,从而可以得到:PA•P B=P C•P D.
(2)如图③所示,当⊙O与射线PM相切于点A,与射线PN相交于C、D两个点.求证:PA2=PC•PD.
【简单应用】
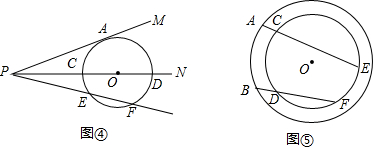
(3)如图④所示,(2)中条件不变,经过点P的另一条射线与⊙O相交于E、F两点.利用上述(1),(2)两问的结论,直接写出线段PA与PE、PF之间的数量关系PA2=PE•PF;当PA=4$\sqrt{3}$,EF=2,则PE=6.
【拓展延伸】
(4)如图⑤所示,在以O为圆心的两个同心圆中,A、B是大⊙O上的任意两点,经过A、B 两点作线段,分别交小⊙O于C、E、D、F四个点.求证:AC•AE=BD•BF.(友情提醒:可直接运用本题上面所得到的相关结论)
分析 (1)由圆内接四边形的性质得出∠PAC=∠PDB,再由∠P=∠P,得出△PAC∽△PDB,得出对应边成比例,即可得出PA•P B=P C•P D;
(2)连接AC、AD,由弦切角定理得出∠PAC=∠PDA,再由∠P=∠P,证出△PAC∽△PDA,得出对应边成比例,即可得出结论;
(3)由(2)得出PA2=PE•PF.代入已知数据得出PE(PE+2)=48,解方程即可;
(4)过A作⊙O的切线AM,M为切点,过B作⊙O的切线BN,N为切点,连接OA、OM、OB、ON,由切线的性质得出AM⊥OM,BN⊥ON,由(3)得:AM2=AC•AE,BN2=BD•BF.在Rt△AOM中,由勾股定理得出AM2=OA2-OM2,在Rt△BON中,由勾股定理得出BN2=OB2-ON2,再由同圆的半径相等,即可得出结论.
解答 (1)解:由圆内接四边形的性质得:∠PAC=∠PDB,
又∵∠P=∠P,
∴△PAC∽△PDB,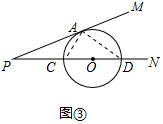
∴PA:PD=PC:PB,
∴PA•P B=P C•P D.
故答案为:△PDB;
(2)证明:连接AC、AD,如图③所示:
∵⊙O与射线PM相切于点A,与射线PN相交于C、D两个点,
∴∠PAC=∠PDA,
又∵∠P=∠P,
∴△PAC∽△PDA,
∴PA:PD=PC:PA,
∴PA2=PC•PD;
(3)解:由(2)得:PA2=PE•PF.
∵PA=4$\sqrt{3}$,EF=2,
∴PE•PF=(4$\sqrt{3}$)2=48,
即PE(PE+2)=48,
解得:PE=6,或PE=-8(舍去),
∴PE=6,
故答案为:PA2=PE•PF,6;
(4)证明:过A作⊙O的切线AM,M为切点,过B作⊙O的切线BN,N为切点,连接OA、OM、OB、ON,则AM⊥OM,BN⊥ON,如图⑤所示:
由(3)得:AM2=AC•AE,BN2=BD•BF.
在Rt△AOM中,AM2=OA2-OM2,
在Rt△BON中,BN2=OB2-ON2,
又∵OM=ON,OA=OB,
∴AM2=BN2,
∴AC•AE=BD•BF.
点评 本题是圆的综合题目,考查了切线的性质、圆内接四边形的性质、弦切角定理、相似三角形的判定与性质、勾股定理等知识;本题综合性强,有一定难度,证明三角形相似是解决问题的关键.

| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 四边相等的四边形是菱形 | |
| C. | 一组对边平行的四边形是平行四边形 | |
| D. | 矩形的对角线互相垂直 |
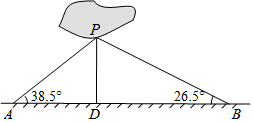 如图,商丘市睢阳区南湖中有一小岛,湖边有一条笔直的观光小道,现决定从小岛架一座与观光小道垂直的小桥PD,小坤在小道上测得如下数据:AB=200.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小坤求出小桥PD的长.(结果精确到0.1米)
如图,商丘市睢阳区南湖中有一小岛,湖边有一条笔直的观光小道,现决定从小岛架一座与观光小道垂直的小桥PD,小坤在小道上测得如下数据:AB=200.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小坤求出小桥PD的长.(结果精确到0.1米)