题目内容
9.某学校为了增强学生体质,决定组建以下体育课外活动小组:A.篮球、B.乒乓球、C.跳绳、D.踢毽子.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:(1)这次被调查的学生共有200人;
(2)喜欢C(跳绳)的学生占总数的百分比为30%;
(3)在平时的训练中,B(乒乓球)小组中的甲、乙、丙、丁四人表现优异,现决定从四人中抽调两人参加比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).

分析 (1)根据A圆心角的度数,求出A所占的百分比,再根据A的人数即可求出这次被调查的学生数;
(2)用喜欢C(跳绳)的学生除以总学生数即可;
(3)根据题意先画出树状图,得出所有等可能性的结果,再根据概率公式即可得出答案.
解答 解:(1)这次被调查的学生共有20÷$\frac{36}{360}$=200(人);
故答案为:200;
(2)喜欢C(跳绳)的学生占总数的百分比为:$\frac{200-20-80-40}{200}$×100%=30%;
故答案为:30%;
(3)画树状图如下: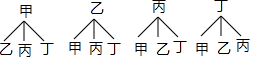
∵共有12种等可能性的结果,恰好选中甲、乙两位同学的有2种,
∴恰好选中甲、乙两位同学的概率是$\frac{2}{12}$=$\frac{1}{6}$.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
17.若一元二次方程2x2-6x+3=0的两根为x1,x2,则x1x2的值为( )
| A. | 3 | B. | 6 | C. | -6 | D. | $\frac{3}{2}$ |
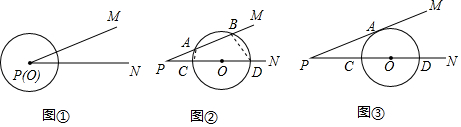
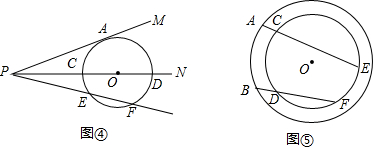
 我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)
我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75) 如图是由3个相同的正方体组成的一个立方体图形,它的三视图是( )
如图是由3个相同的正方体组成的一个立方体图形,它的三视图是( )



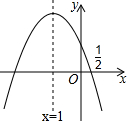 如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点(0.5,0),有下列结论:
如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点(0.5,0),有下列结论: 如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.
如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.