题目内容
 如图,△ABC中,AB=AC,∠A=46°,DE垂直平分AB,△BEC的周长为20,BC=9.
如图,△ABC中,AB=AC,∠A=46°,DE垂直平分AB,△BEC的周长为20,BC=9.(1)求∠EBC的度数;
(2)求△ABC的周长.
考点:线段垂直平分线的性质,等腰三角形的性质
专题:
分析:(1)先根据等腰三角形的性质求出∠ABC的度数,再由线段垂直平分线的性质求出AE=BE,进而得出结论;
(2)先根据△BEC的周长为20,BC=9求出AC的长,进而得出结论.
(2)先根据△BEC的周长为20,BC=9求出AC的长,进而得出结论.
解答:解:(1)∵△ABC中,AB=AC,∠A=46°,
∴∠ABC=
=
=67°,
∵DE垂直平分AB,
∴AE=BE,
∴∠A=∠ABE=46°,
∴∠EBC=∠ABC-∠ABE=67°-46°=21°;
(2)∵△BEC的周长为20,BC=9,
∴BE+CE=20-9=11,
∵AE=BE,
∴AC=11,
∵AB=AC,
∴△ABC的周长=AB+AC+BC=11+11+9=31.
∴∠ABC=
| 180°-∠A |
| 2 |
| 180°-46° |
| 2 |
∵DE垂直平分AB,
∴AE=BE,
∴∠A=∠ABE=46°,
∴∠EBC=∠ABC-∠ABE=67°-46°=21°;
(2)∵△BEC的周长为20,BC=9,
∴BE+CE=20-9=11,
∵AE=BE,
∴AC=11,
∵AB=AC,
∴△ABC的周长=AB+AC+BC=11+11+9=31.
点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
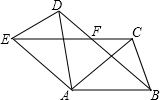 如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°得到△ADE,连接BD,CE交于点F.
如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°得到△ADE,连接BD,CE交于点F. 如图,AB∥DC,∠ABD=30°,∠ADB=85°,求∠ADC和∠A的角度.
如图,AB∥DC,∠ABD=30°,∠ADB=85°,求∠ADC和∠A的角度. 如图,六边形ABCDEF的内角都相等,∠DAB=60°.AB与DE有什么关系?为什么?
如图,六边形ABCDEF的内角都相等,∠DAB=60°.AB与DE有什么关系?为什么?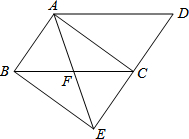 如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.