题目内容
 如图,△ABC的两条中线BE、CD交于点O,连接AO.
如图,△ABC的两条中线BE、CD交于点O,连接AO.(1)在OA上找一点F,使四边形ODFE为平行四边形;
(2)求
| OE |
| OB |
考点:三角形的重心,平行四边形的判定
专题:
分析:(1)连结DE,交OA于P,在OA上取点F,使OF=2OP,连结FD、FE,可证四边形ODFE为平行四边形;
(2)由点O为△ABC的重心,根据重心到顶点的距离与重心到对边中点的距离之比为2:1,可得
=
.
(2)由点O为△ABC的重心,根据重心到顶点的距离与重心到对边中点的距离之比为2:1,可得
| OE |
| OB |
| 1 |
| 2 |
解答: 解:(1)如图,连结DE,交OA于P,在OA上取点F,使OF=2OP,连结FD、FE,得到四边形ODFE.延长AO交BC于Q.
解:(1)如图,连结DE,交OA于P,在OA上取点F,使OF=2OP,连结FD、FE,得到四边形ODFE.延长AO交BC于Q.
∵△ABC的两条中线BE、CD交于点O,延长AO交BC于Q,
∴点O为△ABC的重心,点Q为BC边的中点.
∵点D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,
∴
=
=
,
=
=
,
∴DP=
BQ,PE=
QC,
∵BQ=QC,
∴DP=PE,
∵OF=2OP,
∴OP=PF,
∴四边形ODFE为平行四边形;
(2)∵点O为△ABC的重心,
∴
=
.
 解:(1)如图,连结DE,交OA于P,在OA上取点F,使OF=2OP,连结FD、FE,得到四边形ODFE.延长AO交BC于Q.
解:(1)如图,连结DE,交OA于P,在OA上取点F,使OF=2OP,连结FD、FE,得到四边形ODFE.延长AO交BC于Q.∵△ABC的两条中线BE、CD交于点O,延长AO交BC于Q,
∴点O为△ABC的重心,点Q为BC边的中点.
∵点D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,
∴
| DP |
| BQ |
| AD |
| AB |
| 1 |
| 2 |
| PE |
| QC |
| AE |
| AC |
| 1 |
| 2 |
∴DP=
| 1 |
| 2 |
| 1 |
| 2 |
∵BQ=QC,
∴DP=PE,
∵OF=2OP,
∴OP=PF,
∴四边形ODFE为平行四边形;
(2)∵点O为△ABC的重心,
∴
| OE |
| OB |
| 1 |
| 2 |
点评:本题考查了三角形中位线定理,重心的定义与性质,平行线分线段成比例定理,平行四边形的判定,难度中等.

练习册系列答案
相关题目
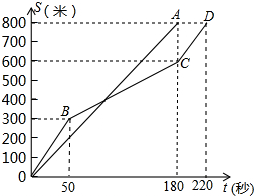 在某市初中学业水平考试体育学科800米能力测试中,某考点同时起跑的甲和乙所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD.下列说法错误的是( )
在某市初中学业水平考试体育学科800米能力测试中,某考点同时起跑的甲和乙所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD.下列说法错误的是( )| A、甲比乙先到达终点 |
| B、跑步过程中甲的速度不变 |
| C、起跑后400米内,乙始终在甲的前面 |
| D、在起跑后180米时,甲乙两人相遇 |
在数轴上表示不等式组
的解,其中正确的是( )
|
A、 |
B、 |
C、 |
D、 |
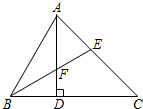 如图,在△ABC中,∠ABC=60°,∠C=45°,AD是BC边上的高,∠ABC的角平分线BE交AD于点F,则图中共有等腰三角形( )
如图,在△ABC中,∠ABC=60°,∠C=45°,AD是BC边上的高,∠ABC的角平分线BE交AD于点F,则图中共有等腰三角形( )| A、2个 | B、3个 | C、4个 | D、5个 |
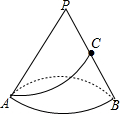 有一个圆锥体形状的粮仓,如图所示,一只猫在A处发现PB中点C处有一只老鼠在偷吃粮食,已知圆锥底面积为25πcm2,母线长为10cm,若猫在粮仓面上捉老鼠,则猫出A点到C点的最短路程是多少?
有一个圆锥体形状的粮仓,如图所示,一只猫在A处发现PB中点C处有一只老鼠在偷吃粮食,已知圆锥底面积为25πcm2,母线长为10cm,若猫在粮仓面上捉老鼠,则猫出A点到C点的最短路程是多少?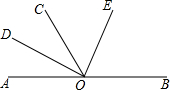 如图:O为直线AB上的一点,∠AOC=60°,OD平分∠AOC,∠DOC与∠COE互余,
如图:O为直线AB上的一点,∠AOC=60°,OD平分∠AOC,∠DOC与∠COE互余,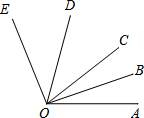 如图,OB是∠AOC的平分线,OD是∠EOC的平分线.
如图,OB是∠AOC的平分线,OD是∠EOC的平分线.