题目内容
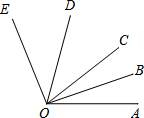 如图,OB是∠AOC的平分线,OD是∠EOC的平分线.
如图,OB是∠AOC的平分线,OD是∠EOC的平分线.(1)如果∠AOD=75°,∠BOC=19°,则∠DOE的度数为
(2)如果∠BOD=56°,求∠AOE的度数.
考点:角平分线的定义
专题:
分析:(1)根据角平分线的定义求得∠AOC=38°,∠DOE=∠DOC=∠AOD-∠AOC=75°-38°=37°;
(2)根据角平分线的定义易求∠AOE=2∠BOD.
(2)根据角平分线的定义易求∠AOE=2∠BOD.
解答:解:(1)∵OB是∠AOC的平分线,∠BOC=19°,
∴∠AOC=2∠BOC=38°,
∴∠DOC=∠AOD-∠AOC=75°-38°=37°.
又∵OD是∠EOC的平分线,
∴∠DOE=∠DOC=37°.
故答案为:37°;
(2)如图,∵OB是∠AOC的平分线,
∴∠AOC=2∠BOC.
∵OD是∠EOC的平分线,
∴∠COE=2∠COD,
∴∠AOE=∠AOC+∠COE
=2∠BOC+2∠COD
=2∠BOD
=112°.
∴∠AOC=2∠BOC=38°,
∴∠DOC=∠AOD-∠AOC=75°-38°=37°.
又∵OD是∠EOC的平分线,
∴∠DOE=∠DOC=37°.
故答案为:37°;
(2)如图,∵OB是∠AOC的平分线,
∴∠AOC=2∠BOC.
∵OD是∠EOC的平分线,
∴∠COE=2∠COD,
∴∠AOE=∠AOC+∠COE
=2∠BOC+2∠COD
=2∠BOD
=112°.
点评:本题考查了角平分线的定义.解题时,实际上是根据角平分线定义得出所求角与已知角的关系转化求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若A=2x2-8x,B=x2+2x+1,则使A-2B=-10的x的值是( )
A、
| ||
| B、3 | ||
C、
| ||
D、
|
 如图,△ABC的两条中线BE、CD交于点O,连接AO.
如图,△ABC的两条中线BE、CD交于点O,连接AO. 如图,已知三点A、B、Q,请画直线AB,并描述点Q和直线AB的位置关系:
如图,已知三点A、B、Q,请画直线AB,并描述点Q和直线AB的位置关系: 如图,已知∠AOB是直角,COD是一条直线,∠AOC=25°,则∠BOD=
如图,已知∠AOB是直角,COD是一条直线,∠AOC=25°,则∠BOD= 已知:如图,BC、AD分别垂直OA、OB,BC和AD相交于E,且OE平分∠AOB,已知CE=3cm,∠A=30°,试求EB的长.
已知:如图,BC、AD分别垂直OA、OB,BC和AD相交于E,且OE平分∠AOB,已知CE=3cm,∠A=30°,试求EB的长.