题目内容
20. 某小学三年级到六年级的全体学生参加“礼仪”知识测试,试题共有10题,每题10分.从中随机抽取了部分学生的成绩进行统计,发现抽测的学生每人至少答对了6题,现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”.
某小学三年级到六年级的全体学生参加“礼仪”知识测试,试题共有10题,每题10分.从中随机抽取了部分学生的成绩进行统计,发现抽测的学生每人至少答对了6题,现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”.成绩情况统计表
| 成绩 | 100分 | 90分 | 80分 | 70分 | 60分 |
| 人数 | 21 | 40 | 36 | 18 | 5 |
| 频率 | 0.175 | 0.333 | 0.3 | 0.15 | 0.04 |
(1)测试学生中,成绩为80分的学生人数有36名;众数是90分;中位数是90分;
(2)若该小学三年级到六年级共有1800名学生,则可估计出成绩为70分的学生人数约有270名.
分析 (1)先由直方图得到调查的学生总数,然后计算出各成绩的人数或频率,再根据众数、中位数的定义求解即可.
(2)利用成绩为70分的学生所占百分数乘以1800即可.
解答 解:(1)学生总人数=28+30+26++36=120(人),
21÷120=0.175,40÷120≈0.333,5÷120≈0.04,0.3×120=36,即成绩为80分的学生人数有36人,120-21-40-36-5=18,18÷120=0.15,
90出现的次数最多,所以众数为90(分),
第60和第61个数都是90分,所以中位数为90分;
(2)1800×0.15=270名.
估计成绩为70分的学生人数约有270名.
故答案为36,18,0.175,0.333,0.15,0.04;36,90,90;270.
点评 本题考查了众数和中位数的知识,属于基础题,解答本题的关键是熟练掌握众数和中位数的定义.

练习册系列答案
相关题目
11. 在直线y=-x+4032的图象上有点P1、P2、P3…、P2014,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段,构成若干个长方形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014,则S1+S2+S3…+S2014=( )
在直线y=-x+4032的图象上有点P1、P2、P3…、P2014,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段,构成若干个长方形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014,则S1+S2+S3…+S2014=( )
 在直线y=-x+4032的图象上有点P1、P2、P3…、P2014,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段,构成若干个长方形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014,则S1+S2+S3…+S2014=( )
在直线y=-x+4032的图象上有点P1、P2、P3…、P2014,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段,构成若干个长方形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014,则S1+S2+S3…+S2014=( )| A. | 8056 | B. | 8050 | C. | 8054 | D. | 8052 |
8. 如图,已知三条直线a、b、c,a∥b,c与a、b交于A、C,点B在b上,∠1=65°,AB=BC,则∠2的度数是( )
如图,已知三条直线a、b、c,a∥b,c与a、b交于A、C,点B在b上,∠1=65°,AB=BC,则∠2的度数是( )
 如图,已知三条直线a、b、c,a∥b,c与a、b交于A、C,点B在b上,∠1=65°,AB=BC,则∠2的度数是( )
如图,已知三条直线a、b、c,a∥b,c与a、b交于A、C,点B在b上,∠1=65°,AB=BC,则∠2的度数是( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
15. 在一个边长不超过8厘米的大正方形ABCD中,如图所示,放入3张面积都是20平方厘米的小正方形纸片BEFG、OPNC、IQKJ,已知3张小正方形纸片盖住的总面积为44平方厘米,那么大正方形ABCD和小正方形BEFG的边长之比为( )
在一个边长不超过8厘米的大正方形ABCD中,如图所示,放入3张面积都是20平方厘米的小正方形纸片BEFG、OPNC、IQKJ,已知3张小正方形纸片盖住的总面积为44平方厘米,那么大正方形ABCD和小正方形BEFG的边长之比为( )
 在一个边长不超过8厘米的大正方形ABCD中,如图所示,放入3张面积都是20平方厘米的小正方形纸片BEFG、OPNC、IQKJ,已知3张小正方形纸片盖住的总面积为44平方厘米,那么大正方形ABCD和小正方形BEFG的边长之比为( )
在一个边长不超过8厘米的大正方形ABCD中,如图所示,放入3张面积都是20平方厘米的小正方形纸片BEFG、OPNC、IQKJ,已知3张小正方形纸片盖住的总面积为44平方厘米,那么大正方形ABCD和小正方形BEFG的边长之比为( )| A. | 5:3 | B. | 3:2 | C. | 10:7 | D. | 8:5 |
12. 已知一次函数y=kx+b的图象如图所示,下列说法中不正确的是( )
已知一次函数y=kx+b的图象如图所示,下列说法中不正确的是( )
 已知一次函数y=kx+b的图象如图所示,下列说法中不正确的是( )
已知一次函数y=kx+b的图象如图所示,下列说法中不正确的是( )| A. | 函数值y随x的增大而减少 | B. | kb<0 | ||
| C. | 当x<1时,y>0 | D. | k+b<0 |
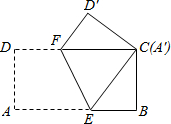 如图,将长为4cm,宽为2cm的矩形纸片ABCD沿着EF翻叠,使点A与C重合,则折痕EF的长为$\sqrt{5}$cm.
如图,将长为4cm,宽为2cm的矩形纸片ABCD沿着EF翻叠,使点A与C重合,则折痕EF的长为$\sqrt{5}$cm. 如图,△A1OB1是边长为1的等边三角形,将其以原点O为中心在原点两侧进行位似变换,得△A2OB2,二者的位似比为1:2,将△A2OB2以x轴为对称轴进行轴对称变换,得△A3OB2再原点O为中心在原点两侧进行位似变换,得△A4OB3,二者的位似比为1:2,按此规律.则点A2016的坐标为($\frac{1}{2}$×4504,$\frac{\sqrt{3}}{2}$×4504).
如图,△A1OB1是边长为1的等边三角形,将其以原点O为中心在原点两侧进行位似变换,得△A2OB2,二者的位似比为1:2,将△A2OB2以x轴为对称轴进行轴对称变换,得△A3OB2再原点O为中心在原点两侧进行位似变换,得△A4OB3,二者的位似比为1:2,按此规律.则点A2016的坐标为($\frac{1}{2}$×4504,$\frac{\sqrt{3}}{2}$×4504).