题目内容
18.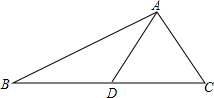 如图所示,在△ABC中,AD是BC边上的中线,且AD=$\frac{1}{2}$BC.
如图所示,在△ABC中,AD是BC边上的中线,且AD=$\frac{1}{2}$BC.(1)求证:∠BAC=90°;
(2)此题的结论实际上是直角三角形的一种判定方法,请你用文字语言叙述出来;
(3)直接运用上面的结论解答下列题目:一个三角形一边长为2,这条边上的中线长为1,另两边之和为1+$\sqrt{3}$,求这个三角形的面积.
分析 (1)由题意易证AD=BD=DC,所以△ADB和△ADC都是等腰三角形,再根据等腰三角形的性质以及三角形内角和定理即可证明∠BAC=90°;
(2)根据直角三角形的判定定理即可得出结论;
(3)设这个直角三角形的两条直角边的长分别为a、b,根据勾股定理可求出ab与a+b的值,再根据直角三角形的面积公式即可得出结论.
解答 (1)证明:∵AD=$\frac{1}{2}$BC,BD=CD=$\frac{1}{2}$BC,
∴AD=BD=DC,
∴△ADB和△ADC都是等腰三角形
∴∠B=∠BAD,∠C=∠CAD,
∵∠B+∠BAD+∠CAD+∠C=180°,
∴∠BAD+∠CAD=90°,
即∠BAC=90°;
(2)根据题意用语言表述为:如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形.
(3))因为这个三角形的一条边上的中线长是这条边长的一半,所以这个三角形是直角三角形.
设这个直角三角形的两条直角边的长分别为a、b,则a+b=1+$\sqrt{3}$
根据勾股定理,得a2+b2=22,即a2+b2=4,
∵(a+b)2=a2+b2+2ab,即(1+$\sqrt{3}$)2=4+2ab,
∴ab=$\sqrt{3}$,
∴S=$\frac{1}{2}$ab=$\frac{\sqrt{3}}{2}$,
∴这个三角形的面积为$\frac{\sqrt{3}}{2}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
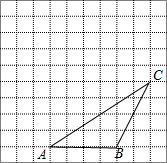 如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.
如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.