题目内容
18. 请在下列括号里填上合适的理由:
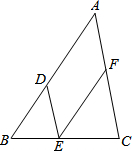
请在下列括号里填上合适的理由:如图,已知DE∥AC,∠A=∠DEF,试说明∠B=∠FEC
证明∵DE∥AC(已知)
∴∠A=∠BDE(两直线平行,同位角相等)
∵∠A=∠DEF(已知)
∴∠BDE=∠DEF(等量代换)
∴AB∥EF (内错角相等,两直线平行)
∴∠B=∠FEC (两直线平行,同位角相等)
分析 根据平行线的性质和判定方法结合图形填空即可.
解答 解:∵DE∥AC(已知)
∴∠A=∠BDE(两直线平行,同位角相等),
∵∠A=∠DEF(已知)
∴∠BDE=∠DEF(等量代换),
∴AB∥EF(内错角相等,两直线平行),
∴∠B=∠FEC(两直线平行,同位角相等).
故答案为:两直线平行,同位角相等;等量代换;内错角相等,两直线平行;两直线平行,同位角相等.
点评 本题考查了平行线的判定与性质,是基础题,主要是逻辑推理能力的训练,熟记平行线的判定方法与性质是解题的关键.

练习册系列答案
相关题目
6.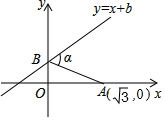 如图,已知A点坐标为($\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=60°,则b的值为( )
如图,已知A点坐标为($\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=60°,则b的值为( )
 如图,已知A点坐标为($\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=60°,则b的值为( )
如图,已知A点坐标为($\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=60°,则b的值为( )| A. | 3$\sqrt{3}$-3 | B. | $\sqrt{3}$+3 | C. | 2$\sqrt{3}$+3 | D. | 2$\sqrt{3}$-3 |
 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2016次相遇地点的坐标是(2,0).
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2016次相遇地点的坐标是(2,0).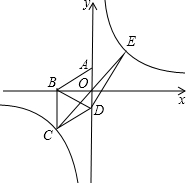 如图,在平面直角坐标系中四边形ABCD为菱形,边AD在y轴上.其中A(0,1),B(-$\sqrt{3}$,0),双曲线y=$\frac{m}{x}$经过点C.
如图,在平面直角坐标系中四边形ABCD为菱形,边AD在y轴上.其中A(0,1),B(-$\sqrt{3}$,0),双曲线y=$\frac{m}{x}$经过点C.