题目内容
在Rt△ABC中,∠C=90°,CD是斜边AB上的高,如果CD=3,BD=2.求cos∠A的值.
 【解析】分析:根据题意画出图形,进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可.
本题解析:
如图所示:
∵∠ACB=90°,∴∠B+∠A=90°,
∵CD⊥AB,∴∠CDA=90°,∴∠B+∠BCD=90°,∴∠BCD=∠A,
∵CD=3,BD=2,∴BC=
∴cosA=cos∠BCD=
故答案为:
【解析】分析:根据题意画出图形,进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可.
本题解析:
如图所示:
∵∠ACB=90°,∴∠B+∠A=90°,
∵CD⊥AB,∴∠CDA=90°,∴∠B+∠BCD=90°,∴∠BCD=∠A,
∵CD=3,BD=2,∴BC=
∴cosA=cos∠BCD=
故答案为:
练习册系列答案
相关题目
已知点M(-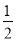 ,3m)关于原点对称的点在第一象限,那么m的取值范围是____________.
,3m)关于原点对称的点在第一象限,那么m的取值范围是____________.
 m<0
【解析】因为点M(,3m)关于原点对称的点在第一象限,所以-3m>0,所以m<0,故答案为:m<0.
m<0
【解析】因为点M(,3m)关于原点对称的点在第一象限,所以-3m>0,所以m<0,故答案为:m<0. 在△ABC中,AB=4a,BC=14,AC=3a.则a的取值范围是 ( )
A. a>2 B. 2<a<14 C. 7<a<14 D. a<14
 B
【解析】试题解析:∵△ABC中,AB=4a,BC=14,AC=3a,
∴解得2
B
【解析】试题解析:∵△ABC中,AB=4a,BC=14,AC=3a,
∴解得2如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为24 cm,△ECF的周长为8 cm,求四边形纸片ABCD的周长.
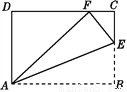
 32(cm)
【解析】根据轴对称的性质可以得到AB=AF,BE=FE,再利用等量代换即可求出四边形纸片ABCD的周长.
解:由题意可知,△ABE和△AFE关于直线AE成轴对称,
所以AB=AF,BE=FE.
因为△AFD的周长为24 cm,△ECF的周长为8 cm,
即AD+DF+AF=24 cm,FC+CE+FE=8 cm,
所以四边形纸片ABCD的周长为:
...
32(cm)
【解析】根据轴对称的性质可以得到AB=AF,BE=FE,再利用等量代换即可求出四边形纸片ABCD的周长.
解:由题意可知,△ABE和△AFE关于直线AE成轴对称,
所以AB=AF,BE=FE.
因为△AFD的周长为24 cm,△ECF的周长为8 cm,
即AD+DF+AF=24 cm,FC+CE+FE=8 cm,
所以四边形纸片ABCD的周长为:
... 如图,已知要在一块长方形的空地上修建一个花坛,要求花坛图案(阴影部分)为轴对称图形,图中的设计符合要求的有( )
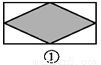
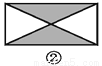
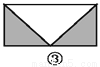
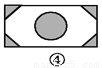
A. 4个 B. 3个 C. 2个 D. 1个
 A
【解析】根据轴对称图形的概念即可判定.
【解析】
四副设计图中的阴影部分均为轴对称图形,故满足设计要求的图形有4个.
故选A.
A
【解析】根据轴对称图形的概念即可判定.
【解析】
四副设计图中的阴影部分均为轴对称图形,故满足设计要求的图形有4个.
故选A. 如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB= .
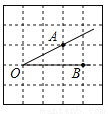
 .
【解析】试题分析:过点A作AD⊥OB垂足为D,如图,在直角△ABD中,AD=1,OD=2,则tan∠AOB==.故答案为: .
.
【解析】试题分析:过点A作AD⊥OB垂足为D,如图,在直角△ABD中,AD=1,OD=2,则tan∠AOB==.故答案为: . 如图,在平面直角坐标系xOy中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )
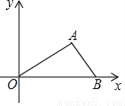
A. 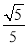 B.
B. 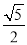 C.
C. 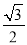 D.
D. 
 A
【解析】试题解析:过A作AC⊥x轴,
∵A(2,1),
∴AC=1,OC=2,
在Rt△AOC中,根据勾股定理得:OA=,
则sin∠AOB=,
故选A
A
【解析】试题解析:过A作AC⊥x轴,
∵A(2,1),
∴AC=1,OC=2,
在Rt△AOC中,根据勾股定理得:OA=,
则sin∠AOB=,
故选A sin70°,cos70°,tan70°的大小关系是( )
A. tan70°<cos70°<sin70° B. cos70°<tan70°<sin70°
C. sin70°<cos70°<tan70° D. cos70°<sin70°<tan70°
 D
【解析】根据锐角三角函数的概念,知sin70°<1,cos70°<1,tan70°>1.
又cos70°=sin20°,正弦值随着角的增大而增大,∴sin70°>cos70°=sin20°.
故选D.
D
【解析】根据锐角三角函数的概念,知sin70°<1,cos70°<1,tan70°>1.
又cos70°=sin20°,正弦值随着角的增大而增大,∴sin70°>cos70°=sin20°.
故选D. 如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成的角为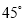 ,如果梯子的底端
,如果梯子的底端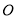 固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为
固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为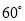 ,求此保管室的宽度
,求此保管室的宽度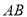 的长.
的长.
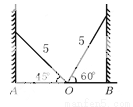
 【解析】由于两边的墙都和地面垂直,所以构成了两个直角三角形.
∵cos45°==,∴;而cos60°==,∴BO=.
∴AB=AO+BO==.
【解析】由于两边的墙都和地面垂直,所以构成了两个直角三角形.
∵cos45°==,∴;而cos60°==,∴BO=.
∴AB=AO+BO==. 
