题目内容
化简: 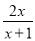 +
+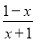 =___.
=___.
 1
【解析】分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可.
解答:【解析】
原式==1.
1
【解析】分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可.
解答:【解析】
原式==1.
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案对于圆的周长公式C=2πR,下列说法中,正确的是( )
A. 2π是变量 B. 2πR是常量 C. C是R的函数 D. 该函数没有定义域
 C
【解析】常量就是在变化过程中不变的量,变量是指在变化过程中随时可以发生变化的量.R是变量,2、π是常量,C是R的函数,该函数的定义域为R>0,故选C.
C
【解析】常量就是在变化过程中不变的量,变量是指在变化过程中随时可以发生变化的量.R是变量,2、π是常量,C是R的函数,该函数的定义域为R>0,故选C. 如图,△ABC的两个外角的平分线相交于点D,如果∠A=50°,那么∠D=_____.
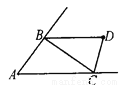
 65°
【解析】试题解析:
故答案为:
65°
【解析】试题解析:
故答案为: 在△ABC中,AB=4a,BC=14,AC=3a.则a的取值范围是 ( )
A. a>2 B. 2<a<14 C. 7<a<14 D. a<14
 B
【解析】试题解析:∵△ABC中,AB=4a,BC=14,AC=3a,
∴解得2
B
【解析】试题解析:∵△ABC中,AB=4a,BC=14,AC=3a,
∴解得2我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则;等等.小学里,把分子比分母小的分数叫做真分数.类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.任何一个假分式都可以化成整式与真分式的和的形式,如: 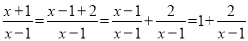 ;
; 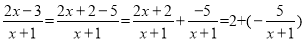
(1)下列分式中,属于真分式的是:________(填序号);
①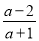 ②
②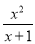 ③
③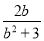 ④
④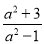
(2)将假分式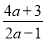 化成整式与真分式的和的形式:
化成整式与真分式的和的形式: 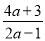 =________+________;
=________+________;
(3)将假分式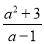 化成整式与真分式的和的形式:
化成整式与真分式的和的形式: 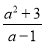 =__________________.
=__________________.
 (1)③;(2)2, ;(3)a+1+ .
【解析】试题分析:(1)认真阅读题意,体会真分式的特点,然后判断即可;
(2)根据题意的化简方法进行化简即可;
(3)根据题意的化简方法进行化简即可.
试题解析:(1)①中的分子分母均为1次,②中分子次数大于分母次数,③分子次数小于分母次数,④分子分母次数一样,故选③.
(2)=,故答案为:2, ;
(3)== ,故答...
(1)③;(2)2, ;(3)a+1+ .
【解析】试题分析:(1)认真阅读题意,体会真分式的特点,然后判断即可;
(2)根据题意的化简方法进行化简即可;
(3)根据题意的化简方法进行化简即可.
试题解析:(1)①中的分子分母均为1次,②中分子次数大于分母次数,③分子次数小于分母次数,④分子分母次数一样,故选③.
(2)=,故答案为:2, ;
(3)== ,故答... 如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为24 cm,△ECF的周长为8 cm,求四边形纸片ABCD的周长.
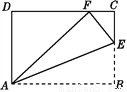
 32(cm)
【解析】根据轴对称的性质可以得到AB=AF,BE=FE,再利用等量代换即可求出四边形纸片ABCD的周长.
解:由题意可知,△ABE和△AFE关于直线AE成轴对称,
所以AB=AF,BE=FE.
因为△AFD的周长为24 cm,△ECF的周长为8 cm,
即AD+DF+AF=24 cm,FC+CE+FE=8 cm,
所以四边形纸片ABCD的周长为:
...
32(cm)
【解析】根据轴对称的性质可以得到AB=AF,BE=FE,再利用等量代换即可求出四边形纸片ABCD的周长.
解:由题意可知,△ABE和△AFE关于直线AE成轴对称,
所以AB=AF,BE=FE.
因为△AFD的周长为24 cm,△ECF的周长为8 cm,
即AD+DF+AF=24 cm,FC+CE+FE=8 cm,
所以四边形纸片ABCD的周长为:
... 如图,已知要在一块长方形的空地上修建一个花坛,要求花坛图案(阴影部分)为轴对称图形,图中的设计符合要求的有( )
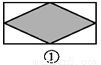
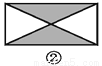
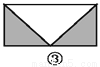
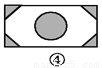
A. 4个 B. 3个 C. 2个 D. 1个
 A
【解析】根据轴对称图形的概念即可判定.
【解析】
四副设计图中的阴影部分均为轴对称图形,故满足设计要求的图形有4个.
故选A.
A
【解析】根据轴对称图形的概念即可判定.
【解析】
四副设计图中的阴影部分均为轴对称图形,故满足设计要求的图形有4个.
故选A. 如图,在平面直角坐标系xOy中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )
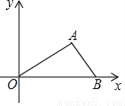
A. 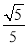 B.
B. 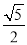 C.
C. 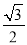 D.
D. 
 A
【解析】试题解析:过A作AC⊥x轴,
∵A(2,1),
∴AC=1,OC=2,
在Rt△AOC中,根据勾股定理得:OA=,
则sin∠AOB=,
故选A
A
【解析】试题解析:过A作AC⊥x轴,
∵A(2,1),
∴AC=1,OC=2,
在Rt△AOC中,根据勾股定理得:OA=,
则sin∠AOB=,
故选A 如图,∠1=∠2,P为BN上一点,且PD⊥BC于点D,AB+BC=2BD.试说明:∠BAP+∠BCP=180°.

 见解析
【解析】作PE垂直于AB于E,根据角平分线的性质可知PD=PE,HL定理可知△PBD≌△PBE,可得BD=BE,根据题中线段和差的关系,可得△PAE≌△PCD,所以可知∠PAE=∠PCD,根据∠PAE+∠PAB=180°,即可证明题中关系.
证明:如图,过点P作PE⊥BA于E.
∵PD⊥BC,PE⊥BM,∠1=∠2,
∴PD=PE.
∵PD⊥BC,PE⊥BM,...
见解析
【解析】作PE垂直于AB于E,根据角平分线的性质可知PD=PE,HL定理可知△PBD≌△PBE,可得BD=BE,根据题中线段和差的关系,可得△PAE≌△PCD,所以可知∠PAE=∠PCD,根据∠PAE+∠PAB=180°,即可证明题中关系.
证明:如图,过点P作PE⊥BA于E.
∵PD⊥BC,PE⊥BM,∠1=∠2,
∴PD=PE.
∵PD⊥BC,PE⊥BM,... 
