题目内容
18.某数学活动小组在一次活动中,对一个数学问题作如下探究:问题发现:如图1,在等边三角形ABC中,点M是边BC上任意一点,连接AM,以AM为边作等边三角形AMN,连接CN,证明:BM=CN.
变式探究:如图2,在等腰三角形ABC中,BA=BC,∠ABC=∠α,点M为边BC上任意一点,以AM为腰作等腰三角形AMN,MA=MN,使∠AMN=∠ABC,连接CN,请求出$\frac{CN}{BM}$的值.(用含α的式子表示出来)
解决问题:如图3,在正方形ADBC中,点M为边BC上一点,以AM为边作正方形作AMEF,N为正方形AMEF的中心,连接CN,若正方形AMEF的边长为$\sqrt{10}$,CN=$\sqrt{2}$,请你求正方形ADBC的边长.
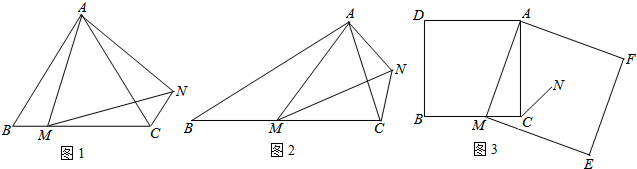
分析 问题发现:根据△ABC,△AMN为等边三角形,得到AB=AC,AM=AN且∠BAC=∠MAN=60°从而得到∠BAC-∠CAM=∠MAN-∠CAM,即∠BAM=∠CAN,证明△BAM≌△CAN,即可得到BM=CN.
变式探究:根据△ABC,△AMN为等腰三角形,得到$\frac{AB}{BC}=\frac{AM}{MN}$=1且∠ABC=∠AMN,证明△ABC~△AMN,得到$\frac{AB}{AM}=\frac{AC}{AN}$,利用等腰三角形的性质BA=BC,得到$∠BAC=\frac{18{0}^{°}-α}{2}$,$∠MAN=\frac{18{0}^{°}-α}{2}$,证明△ABM~△ACN,得到$\frac{CN}{BM}=\frac{AC}{AB}$,作BD⊥AC,如图2,再由AB=BC,得到∠ABD=$\frac{α}{2}$,根据sin∠ABD=$\frac{AD}{AB}=\frac{CD}{BC}=sin\frac{α}{2}$,得到AD=AB•sin$\frac{α}{2}$,则AC=2AD=2ABsin$\frac{α}{2}$,从而得到$\frac{CN}{BM}=\frac{AC}{AB}$=2sin$\frac{α}{2}$.
解决问题:利用四边形ADBC,AMEF为正方形,得到∠ABC=∠BAC=45°∠MAN=45°,即∠BAM=∠CAN,由$\frac{AB}{AC}=\frac{AM}{AN}=\sqrt{2}$,得到$\frac{AB}{AM}=\frac{AC}{AN}$,证明△ABM~△ACN,得到$\frac{BM}{CN}=\frac{AB}{AC}$,进而得到$\frac{CN}{BM}=\frac{AC}{AB}$=cos45°=$\frac{\sqrt{2}}{2}$,求出BM=2,设AC=x,利用勾股定理,在Rt△AMC,AC2+CM2=AM2,即x2+(x-2)2=10,解得:x1=3,x2=-1(舍去),即可解答.
解答 解:问题发现,
∵△ABC,△AMN为等边三角形,
∴AB=AC,AM=AN且∠BAC=∠MAN=60°
∴∠BAC-∠CAM=∠MAN-∠CAM,
∴∠BAM=∠CAN,
在△BAM与△CAN中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAM=∠CAN}\\{AM=AN}\end{array}\right.$,
∴△BAM≌△CAN,
∴BM=CN.
变式探究:∵$\frac{AB}{BC}=\frac{AM}{MN}$=1且∠ABC=∠AMN,
∴△ABC~△AMN,
∴$\frac{AB}{AM}=\frac{AC}{AN}$,
∵AB=BC,
∴$∠BAC=\frac{18{0}^{°}-α}{2}$,
∵AM=MN
∴$∠MAN=\frac{18{0}^{°}-α}{2}$,
∴∠BAM=∠CAN,
∴△ABM~△ACN,
∴$\frac{CN}{BM}=\frac{AC}{AB}$,
作BD⊥AC,如图2,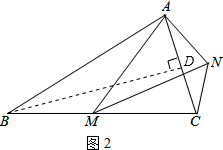
∵AB=BC,
∴∠ABD=$\frac{α}{2}$,
∴sin∠ABD=$\frac{AD}{AB}=\frac{CD}{BC}=sin\frac{α}{2}$,
∴AD=AB•sin$\frac{α}{2}$
∴AC=2AD=2ABsin$\frac{α}{2}$,
∴$\frac{CN}{BM}=\frac{AC}{AB}$=2sin$\frac{α}{2}$
解决问题:
如图3,连接AB,AN.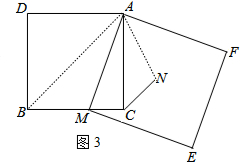
∵四边形ADBC,AMEF为正方形,
∴∠ABC=∠BAC=45°∠MAN=45°,
∴∠BAC-∠MAC=∠MAN-∠MAC
即∠BAM=∠CAN,
∵$\frac{AB}{AC}=\frac{AM}{AN}=\sqrt{2}$,
∴$\frac{AB}{AM}=\frac{AC}{AN}$,
∴△ABM~△ACN,
∴$\frac{BM}{CN}=\frac{AB}{AC}$
∴$\frac{CN}{BM}=\frac{AC}{AB}$=cos45°=$\frac{\sqrt{2}}{2}$,
∴$\frac{\sqrt{2}}{BM}=\frac{\sqrt{2}}{2}$
∴BM=2,
设AC=x,
在Rt△AMC,
AC2+CM2=AM2
即x2+(x-2)2=10,
解得:x1=3,x2=-1(舍去),
答:边长为3.
点评 本题考查了等边三角形的性质、等腰三角形的性质、全等三角形的性质定理和判定定理、相似三角形的性质定理和判定定理,解决本题的关键是相似三角形的判定,在(3)中注意方程思想在勾股定理中应用.

 名校课堂系列答案
名校课堂系列答案| A. | 图象经过点(1,1) | B. | 图象位于第一、三象限 | ||
| C. | 图象是中心对称图形 | D. | 当x<0时,y随x的增大而减小 |
| A. | $\frac{x-1}{{x}^{2}}$ | B. | $\frac{x+1}{{x}^{2}-2}$ | C. | $\frac{x+1}{-{x}^{2}-1}$ | D. | $\frac{2x-1}{x+3}$ |
 如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为50°.
如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为50°.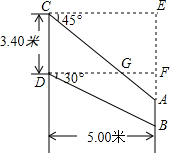 某型号飞机的机翼形状如图,根据图示尺寸计算AC和AB的长度(精确到0.1米,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73 ).
某型号飞机的机翼形状如图,根据图示尺寸计算AC和AB的长度(精确到0.1米,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73 ). 如图.AF∥ED∥BC,AB∥EF∥DC,用一条直线平分图面积.简单描述作法.
如图.AF∥ED∥BC,AB∥EF∥DC,用一条直线平分图面积.简单描述作法.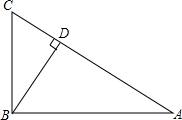 如图,在Rt△ABC中,∠ABC=90°,BD是AC边上的高,已知BC=5厘米,AC=13厘米.求:
如图,在Rt△ABC中,∠ABC=90°,BD是AC边上的高,已知BC=5厘米,AC=13厘米.求: