若点A都在二次函数y=mx2图象上.则a.b.c的大小关系是( )A．c＜a＜bB．b＜a＜cC．a＜b＜cD．c＜b＜a 题目和参考答案——青夏教育精英家教网—

题目内容

2．若点A（-2，a）、B（-1，b）、C（3，c）都在二次函数y=mx²（m＜0）图象上，则a、b、c的大小关系是（　　）

A．

c＜a＜b

B．

b＜a＜c

C．

a＜b＜c

D．

c＜b＜a

分析先根据二次函数的性质得到抛物线的对称轴为y轴，然后比较三个点离对称轴的远近得到a、b、c的大小关系．

解答解：∵二次函数y=mx²（m＜0）
∴抛物线的对称轴为y轴，
∵A（-2，a）、B（-1，b）、C（3，c）
∴点C离y轴最远，点B离y轴最近，
而抛物线开口向下，
∴b＞a＞c；
故选A．

点评本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．

练习册系列答案

a²+a⁵=a⁷

（a²）⁵=a¹⁰

$\sqrt{5}$×2$\sqrt{5}$=12$\sqrt{5}$

17．等腰三角形有一个外角是100°，这个等腰三角形的底角是50°或80°．

7．

如图，点P是⊙O外一点，PA为⊙O的切线，A为切点，直线PO交⊙O于点E、F，弦AB⊥PF，垂足为D，延长BO交⊙O于点C，连接AC，BF．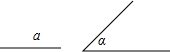
（1）求证：PB与⊙O相切；
（2）若AC=12，tan∠F=$\frac{1}{2}$，求⊙O的直径．

14．

（1）已知：线段a，∠α．求作：△ABC，使BC=a，∠C=∠B=∠α．（不写作法，保留作图痕迹）
（2）在（1）的图形中，如果BC=6$\sqrt{3}$，∠α=30°，求△ABC的面积．

11．

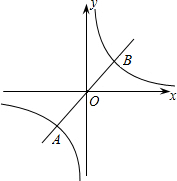如图，已知正比例函数y=2x和反比例函数y=$\frac{k}{x}$（k≠0）的图象交于A、B两点，若A点的纵坐标为-2．
（1）求反比例函数的解析式和点B坐标；
（2）根据图象，直接写出正比例函数值大于反比例函数值时自变量x的取值范围；
（3）若C是双曲线上的动点，D是x轴上的动点，是否存在这样的点C和点D，使以A、B、CD为顶点的四边形是平行四边形？若存在，求出C、D坐标；若不存在，请说明理由．

12．

正方形ABCD的边长为6cm，点E在AE上，AE=2cm，动点F由点C开始以3cm/s的速度沿折线CBE移动，动点G同时由点D开始以1cm/s沿点DC移动2.5秒后以点D、G、F、E为顶点的四边形是平行四边形．

试题分类