题目内容
设a、b是相异的两个实数，且满足a2=4a+3，b2=4b+3，求
+
的值．
| a2 |
| b |
| b2 |
| a |
考点：根与系数的关系
专题：
分析：根据题意可得a+b=4，ab=-3，代入
+
整理后的分式即可求得结果．
| a2 |
| b |
| b2 |
| a |
解答：解：根据题意，得：a+b=4，ab=-3，
∴
+
=
+
=4×（
）+3×
=4×
+3×
=4×
+3×
=-
．
∴
| a2 |
| b |
| b2 |
| a |
| 4a+3 |
| b |
| 4b+3 |
| a |
=4×（
| a2+b2 |
| ab |
| a+b |
| ab |
=4×
| 4(a+b)+6 |
| ab |
| a+b |
| ab |
=4×
| 4×4+6 |
| -3 |
| 4 |
| -3 |
=-
| 100 |
| 3 |
点评：本题考查的是用一元二次方程的求根公式解分式的值，根据题意得出a+b=4，ab=-3，是关键．
练习册系列答案
阅读快车系列答案
相关题目
若函数y=
（k为非零常数）的图象在第二、四象限内，则函数y=kx2+x-2的图象在（ ）
| k |
| x |
A、直线y=-
| ||
B、直线y=-
| ||
C、直线x=-
| ||
D、直线x=-
|
已知，AB是⊙O的直径，半径CO⊥AB，过OC的中点H作EF∥AB，求∠EBA的度数．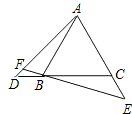
如图，点D、E分别在等边△ABC的边CB、AC为延长线上，且BD=CE，连接EB且延长交AD于F，求证：∠AFB=60°．
如图，△ABC中，AB=AC=5，sinB=