题目内容
17.已知在Rt△ABC中,∠C=90°,若a+b=12cm,c=10cm,则Rt△ABC的面积是( )| A. | 48cm2 | B. | 24cm2 | C. | 16cm2 | D. | 11cm2 |
分析 直接利用勾股定理得出a2+b2的值,再利用完全平方公式得出ab的值,进而得出答案.
解答 解:∵在Rt△ABC中,a2+b2=c2=100,
∵a+b=12cm,c=10cm,
∴(a+b)2=a2+b2+2ab=144,
∴100+2ab=144,
则:$\frac{1}{2}$ab=11,
故Rt△ABC的面积是:11cm2.
故选:D.
点评 此题主要考查了勾股定理以及完全平方公式的应用,得出a2+b2的值是解题关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
8.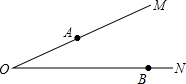 如图,∠MON=20°,A、B分别为射线OM、ON上两定点,且OA=2,OB=4,点P、Q分别为射线OM、ON两动点,当P、Q运动时,线段AQ+PQ+PB的最小值是( )
如图,∠MON=20°,A、B分别为射线OM、ON上两定点,且OA=2,OB=4,点P、Q分别为射线OM、ON两动点,当P、Q运动时,线段AQ+PQ+PB的最小值是( )
 如图,∠MON=20°,A、B分别为射线OM、ON上两定点,且OA=2,OB=4,点P、Q分别为射线OM、ON两动点,当P、Q运动时,线段AQ+PQ+PB的最小值是( )
如图,∠MON=20°,A、B分别为射线OM、ON上两定点,且OA=2,OB=4,点P、Q分别为射线OM、ON两动点,当P、Q运动时,线段AQ+PQ+PB的最小值是( )| A. | 3 | B. | 3$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
20.下列说法正确的是( )
| A. | 若a>b,则ac2>bc2 | B. | 若ac2>bc2,则a>b | C. | 若a>b,则a2>b2 | D. | 若a>b,则$\frac{1}{a}$<$\frac{1}{b}$ |
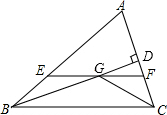 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论: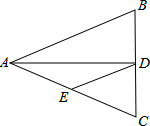 如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )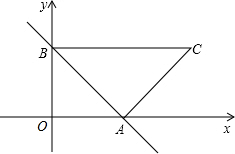 如图,已知在直角坐标系中,A(4,0),B(0,3),以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.点P是x轴上的一个动点,设P(x,0).
如图,已知在直角坐标系中,A(4,0),B(0,3),以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.点P是x轴上的一个动点,设P(x,0).