题目内容
9.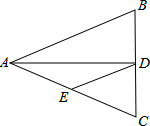 如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )| A. | 20 | B. | 14 | C. | 13 | D. | 12 |
分析 根据AB=AC,可知△ABC为等腰三角形,由等腰三角形三线合一的性质可得AD⊥BC,AD为△ABC的中线,故CD=$\frac{1}{2}$BC,∠ADC=90°,又因为点E为AC的中点,可得DE=$\frac{1}{2}BC$,从而可以得到△CDE的周长.
解答 解:∵AB=AC,
∴△ABC是等腰三角形.
又∵AD平分∠BAC,
∴AD⊥BC,AD是△ABC的中线,点E为AC的中点.
∴∠ADC=90°,AC=2DE,AE=EC.
∵AB=AC=10,BC=8,
∴DE=5,CD=4,CE=5.
∴△CDE的周长为:DE+EC+CD=5+5+4=14.
故选项A错误,故选项B正确,故选项C错误,故选项D错误.
故选B.
点评 本题考查三角形的周长,等腰三角形的相关性质,直角三角形斜边上的中线等于斜边的一半,关键是正确分析题目,从中得出需要的信息.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.下列说法正确的是( )
| A. | $\frac{π}{3}$是分数 | B. | 1的平方根是1 | ||
| C. | 无理数都是无限小数 | D. | 有理数与数轴上的点一一对应 |
17.已知在Rt△ABC中,∠C=90°,若a+b=12cm,c=10cm,则Rt△ABC的面积是( )
| A. | 48cm2 | B. | 24cm2 | C. | 16cm2 | D. | 11cm2 |
14.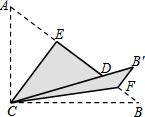 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
12.$\frac{2x}{5x+1}$=$\frac{2x(x+4)}{(5x+1)(x+4)}$成立的条件是( )
| A. | x>-4 | B. | x<-4 | C. | x≠-4 | D. | x>0 |
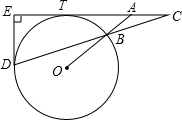 如图,已知等腰三角形ABC,AB=AC,O为AB延长线上的点,以⊙O为圆心,OB为半径作O,交CB的延长线于D,⊙O与直线AC切于点T,作DE⊥AC,垂足为E.
如图,已知等腰三角形ABC,AB=AC,O为AB延长线上的点,以⊙O为圆心,OB为半径作O,交CB的延长线于D,⊙O与直线AC切于点T,作DE⊥AC,垂足为E.