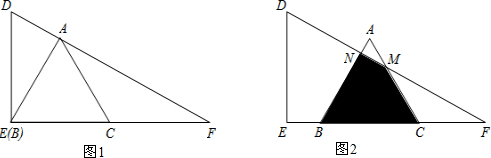Question

6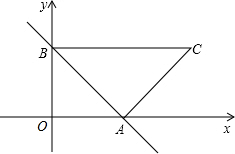．如图，已知在直角坐标系中，A（4，0），B（0，3），以线段AB为直角边在第一象限内作等腰Rt△ABC，∠BAC=90°．点P是x轴上的一个动点，设P（x，0）．
（1）求△ABC的面积；
（2）求点C的坐标；
（3）是否存在这样的点P，使得|PC-PB|的值最大？如果不存在，请说明理由；如果存在，请标出点P的位置．

Answer 1

分析 （1）由点A与B的坐标，根据勾股定理得出AB的长，又由等腰Rt△ABC，且∠BAC=90°，即可求得AC的值，则可求得△ABC的面积，继而求得答案．
（2）过点C作CH⊥x轴于点H，如图1，易证△AOB≌△CHA，从而得到AH、CH，就可得到点C的坐标；
（3）存在这样的P点．当PB与PA成一直线时，|PC-PB|的值最大．

解答 解：（1）∵点A的坐标为：（4，0），点B的坐标为：（0，3），
可得：OB=3，OA=4，
∴在Rt△OAB中，AB=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∴AC=AB=5，
∴S△ABC=$\frac{1}{2}$×AB×AC=$\frac{1}{2}$×5×5=12.5．
（2）过点C作CH⊥x轴于点H，如图1，

则∠AHC=90°．
∴∠AOB=∠BAC=∠AHC=90°，
∴∠OAB=180°-90°-∠HAC=90°-∠HAC=∠HCA．
在△AOB和△CHA中，
$\left\{\begin{array}{l}{∠AOB=∠CHA}\\{∠OAB=∠HCA}\\{AB=CA}\end{array}\right.$，
∴△AOB≌△CHA（AAS），
∴AO=CH=4，OB=HA=3，
∴OH=OA+AH=7，
∴点C的坐标为（7，4）；
（3）存在这样的P点．当PB与PA成一直线时，|PC-PB|的值最大，
如图2，

点评 本题主要考查了一次函数图象上点的坐标特征、全等三角形的判定与性质、勾股定理、三角形的面积公式等知识，构造全等三角形是解决第（2）小题的关键．