题目内容
8.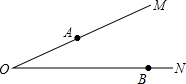 如图,∠MON=20°,A、B分别为射线OM、ON上两定点,且OA=2,OB=4,点P、Q分别为射线OM、ON两动点,当P、Q运动时,线段AQ+PQ+PB的最小值是( )
如图,∠MON=20°,A、B分别为射线OM、ON上两定点,且OA=2,OB=4,点P、Q分别为射线OM、ON两动点,当P、Q运动时,线段AQ+PQ+PB的最小值是( )| A. | 3 | B. | 3$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
分析 首先作A关于ON的对称点A′,点B关于OM的对称点B′,连接A′B′,交于OM,ON分别为P,Q,连接OA′,OB′,可求得AQ+PQ+PB=A′Q+PQ+PB′=A′B′,∠A′OB′=60°,然后由特殊角的三角函数值,判定∠OA′B′=90°,再利用勾股定理求得答案.
解答  解:作A关于ON的对称点A′,点B关于OM的对称点B′,连接A′B′,交于OM,ON分别为P,Q,连接OA′,OB′,
解:作A关于ON的对称点A′,点B关于OM的对称点B′,连接A′B′,交于OM,ON分别为P,Q,连接OA′,OB′,
则PB′=PB,AQ=A′Q,OA′=OA=2,OB′=OB=4,∠MOB′=∠NOA′=∠MON=20°,
∴AQ+PQ+PB=A′Q+PQ+PB′=A′B′,∠A′OB′=60°,
∵cos60°=$\frac{1}{2}$,$\frac{OA′}{OB′}$=$\frac{1}{2}$,
∴∠OA′B′=90°,
∴A′B′=$\sqrt{OB{′}^{2}-OA{′}^{2}}$=2$\sqrt{3}$,
∴线段AQ+PQ+PB的最小值是:2$\sqrt{3}$.
故选D.
点评 此题考查了最短路径问题以及勾股定理.注意准确找到P,Q的位置是解此题的关键.

练习册系列答案
相关题目
20.下列说法正确的是( )
| A. | $\frac{π}{3}$是分数 | B. | 1的平方根是1 | ||
| C. | 无理数都是无限小数 | D. | 有理数与数轴上的点一一对应 |
17.已知在Rt△ABC中,∠C=90°,若a+b=12cm,c=10cm,则Rt△ABC的面积是( )
| A. | 48cm2 | B. | 24cm2 | C. | 16cm2 | D. | 11cm2 |
 如图,是在一个直角三角尺中去掉一半径为r的圆,则阴影部分面积为$\frac{1}{2}$ab-πr2.
如图,是在一个直角三角尺中去掉一半径为r的圆,则阴影部分面积为$\frac{1}{2}$ab-πr2. 如图,已知EC=AC,∠BCE=∠DCA,∠A=∠E,则线段BC与DC相等吗?为什么?
如图,已知EC=AC,∠BCE=∠DCA,∠A=∠E,则线段BC与DC相等吗?为什么?