题目内容
5.混合运算:(1)($\sqrt{48}$-$\sqrt{12}$)÷$\sqrt{3}$×$\frac{1}{\sqrt{3}}$;
(2)3$\sqrt{2}$×$\sqrt{\frac{2}{3}}$-$\sqrt{(\frac{\sqrt{3}}{2}-1)^{2}}$+$\frac{1}{\sqrt{5}+2}$.
分析 (1)先化简算减法,再算乘除;
(2)先化简和计算乘法,再进一步合并即可.
解答 解:(1)原式=2$\sqrt{3}$÷$\sqrt{3}$×$\frac{1}{\sqrt{3}}$
=2×$\frac{1}{\sqrt{3}}$
=$\frac{2\sqrt{3}}{3}$;
(2)原式=2$\sqrt{3}$-(1-$\frac{\sqrt{3}}{2}$)+$\sqrt{5}$-2
=$\frac{5\sqrt{3}}{2}$)+$\sqrt{5}$-3.
点评 本题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列说法正确的是( )
| A. | $\frac{π}{3}$是分数 | B. | 1的平方根是1 | ||
| C. | 无理数都是无限小数 | D. | 有理数与数轴上的点一一对应 |
10.已知一元二次方程mx2+n=0(m≠0),若方程有解,则必须( )
| A. | n=0 | B. | mn同号 | C. | n是m的整数倍 | D. | mn异号 |
17.已知在Rt△ABC中,∠C=90°,若a+b=12cm,c=10cm,则Rt△ABC的面积是( )
| A. | 48cm2 | B. | 24cm2 | C. | 16cm2 | D. | 11cm2 |
14.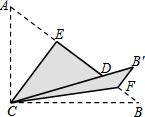 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
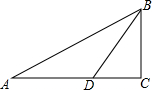 如图,在△ABC中,∠C=90°,BD平分∠ABC,BC=3cm,AC=4cm,则△ABD与△BDC的面积之比为5:3.
如图,在△ABC中,∠C=90°,BD平分∠ABC,BC=3cm,AC=4cm,则△ABD与△BDC的面积之比为5:3. 如图,是在一个直角三角尺中去掉一半径为r的圆,则阴影部分面积为$\frac{1}{2}$ab-πr2.
如图,是在一个直角三角尺中去掉一半径为r的圆,则阴影部分面积为$\frac{1}{2}$ab-πr2. 如图,已知EC=AC,∠BCE=∠DCA,∠A=∠E,则线段BC与DC相等吗?为什么?
如图,已知EC=AC,∠BCE=∠DCA,∠A=∠E,则线段BC与DC相等吗?为什么?