��Ŀ����
3����֪��ƽ��ֱ������ϵxOy�У�OΪ����ԭ�㣬�߶�AB�������˵�A��0��2����B��1��0���ֱ���y���x����������ϣ���CΪ�߶�AB���е㣮�ֽ��߶�BA�Ƶ�B��˳ʱ�뷽����ת90��õ��߶�BD��������y=ax2+bx+c��a��0��������D����1����ͼ1�����������߾���ԭ��O����a=-$\frac{1}{3}$��
�����D�����꼰�������ߵĽ���ʽ��
������CD���ʣ������������Ƿ���ڵ�P��ʹ�á�POB���BCD���ࣿ�����ڣ�������������������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��2����ͼ2������������y=ax2+bx+c��a��0��������E��1��1������Q���������ϣ��������QOB���BCD���࣮������������Q��ĸ�����4������ֱ��д��a��ȡֵ��Χ��

���� ��1���ٹ���D��DF��x���ڵ�F����ͨ��������ȫ�����D�����꣬��D�������a=-$\frac{1}{3}$��c=0����y=ax2+bx+c������������ߵĽ���ʽ��
����֤��CD��x�ᣬ�������Ҫʹ�á�POB���BCD���࣬������POB=��BAO����P������Ϊ��x��-$\frac{1}{3}$x2+$\frac{4}{3}$x����������������ۼ�����ã�
��2��������������Q��ĸ�����4������a��0ʱ�������߽���y��ĸ����ᣬ��a��0ʱ����Сֵ�ã�-1���ⲻ��ʽ������ã�
��� �⣺��1���ٹ���D��DF��x���ڵ�F����ͼ1��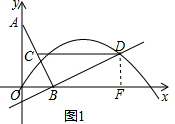
�ߡ�DBF+��ABO=90�㣬��BAO+��ABO=90�㣬
���DBF=��BAO��
�֡ߡ�AOB=��BFD=90�㣬AB=BD��
�ڡ�AOB�͡�BFD�У�
$\left\{\begin{array}{l}{��DBF=��BAO}\\{��AOB=��BFD}\\{AB=BD}\end{array}\right.$��
���AOB�ա�BFD��AAS��
��DF=BO=1��BF=AO=2��
��D�������ǣ�3��1����
�������⣬��a=-$\frac{1}{3}$��c=0����a��32+b��3+c=1��
��b=$\frac{4}{3}$��
��������ߵĽ���ʽΪy=-$\frac{1}{3}$x2+$\frac{4}{3}$x��
�ڡߵ�A��0��2����B��1��0������CΪ�߶�AB���е㣬
��C��$\frac{1}{2}$��1����
��C��D����������궼Ϊ1��
��CD��x�ᣬ
���BCD=��ABO
���BAO���BCD���࣬
Ҫʹ�á�POB���BCD���࣬������POB=��BAO��
��P��������x��-$\frac{1}{3}$x2+$\frac{4}{3}$x����
����P��x����Ϸ�ʱ����P��PG��x���ڵ�G����ͼ2��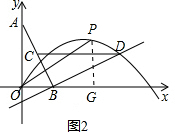
��tan��POB=tan��BAO����$\frac{PG}{OG}$=$\frac{BO}{AO}$��
��$\frac{\frac{1}{3}{x}^{2}-\frac{4}{3}x}{x}$=$\frac{1}{2}$�����x1=0����ȥ����x2=$\frac{5}{2}$��
��-$\frac{1}{3}$x2+$\frac{4}{3}$x=$\frac{5}{4}$��
��P���������$\frac{5}{2}$��$\frac{5}{4}$����
����P��x����·�ʱ����P��PG��x���ڵ�G����ͼ3��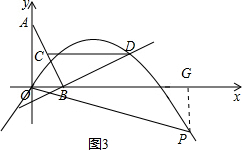
��tan��POB=tan��BAO����p$\frac{PG}{OG}=\frac{BO}{AO}$��
��$\frac{\frac{1}{3}{x}^{2}-\frac{4}{3}x}{x}=\frac{1}{2}$��
���x1=0����ȥ����x2=$\frac{11}{2}$��
��$-\frac{1}{3}$x2+$\frac{4}{3}$x=-$\frac{11}{4}$��
��P���������$\frac{11}{2}$��-$\frac{11}{4}$����
���ϣ����������ϴ��ڵ�P��$\frac{5}{2}$��$\frac{5}{4}$����$\frac{11}{2}$��-$\frac{11}{4}$����ʹ�á�POB���BCD���࣮
��2����ͼ3��ͼ4��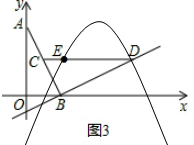
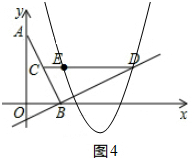
��D��3��1����E��1��1����
������y=ax2+bx+c����E��D������ɵ�$\left\{\begin{array}{l}{a+b+c=1}\\{9a+3b+c=1}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=-4a}\\{c=1+3a}\end{array}\right.$��
����y=ax2-4ax+3a+1��
�����������
�ٵ�������y=ax2+bx+c��������ʱ���������QOB���BCD�����ҷ���������Q��ĸ�����4�������Q��x����ϡ��·�����������
��i������Q��x����Ϸ�ʱ��ֱ��OQ�����������������㣬����������Q��2����
��ii������Q��x����·�ʱ��Ҫʹֱ��OQ��������y=ax2+bx+c���������㣬������y=ax2+bx+c��x��Ľ��������x����������ϣ���y��Ľ�����y��ĸ����ᣬ����3a+1��0�����a��-$\frac{1}{3}$��
�ڵ�������y=ax2+bx+c��������ʱ����Q��x����ϡ��·�����������
��i������Q��x����Ϸ�ʱ��ֱ��OQ��������y=ax2+bx+c���������㣬���������ĵ�Q��������
��ii������Q��x����·�ʱ��Ҫʹֱ��OQ��������y=ax2+bx+c���������㣬���������ĵ�Q��������
���ݣ�2����֪��Ҫʹ�á�QOB���BCD���࣬������QOB=��BAO��
��tan��QOB=tan��BAO=$\frac{OB}{OA}$=$\frac{1}{2}$����ʱֱ��OQ��б��Ϊ-$\frac{1}{2}$����ֱ��OQ�Ľ���ʽΪy=-$\frac{1}{2}$x��Ҫʹֱ��OQ��������y=ax2+bx+c���������㣬���Է���ax2-4ax+3a+1=-$\frac{1}{2}$x����������ȵ�ʵ���������ԡ�=��-4a+$\frac{1}{2}$��2-4a��3a+1����0����4a2-8a+$\frac{1}{4}$��0�����a��$\frac{4+\sqrt{15}}{4}$��a��$\frac{4-\sqrt{15}}{4}$��ȥ��
������ʾ��a��ȡֵ��ΧΪa��-$\frac{1}{3}$��a��$\frac{4+\sqrt{15}}{4}$��
���� �����Ƕ��κ������ۺ��⣬�����˴���ϵ��������κ����Ľ���ʽ�����к�������Сֵ�ȣ��������۵�˼���DZ���Ĺؼ���

 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д� ��ֱ�ߺ�ֱ�����ǰ尴��ͼλ�ðڷţ�����1=25�㣬���2�Ķ����ǣ�������
��ֱ�ߺ�ֱ�����ǰ尴��ͼλ�ðڷţ�����1=25�㣬���2�Ķ����ǣ�������| A�� | 35�� | B�� | 45�� | C�� | 55�� | D�� | 65�� |
 ��ͼ��ͼ�����ⳤΪ4cm�������壬��������������ĶԽ��ߣ����ߣ��õ�һ���ǣ��õ���ͼ�ڵļ����壬��һֻ��������ͼ�ڼ�����ı��棬�Ӷ���A��������B����̾���Ϊ��2$\sqrt{2}$+2$\sqrt{6}$��cm��
��ͼ��ͼ�����ⳤΪ4cm�������壬��������������ĶԽ��ߣ����ߣ��õ�һ���ǣ��õ���ͼ�ڵļ����壬��һֻ��������ͼ�ڼ�����ı��棬�Ӷ���A��������B����̾���Ϊ��2$\sqrt{2}$+2$\sqrt{6}$��cm�� ��֪�������������ϵ�λ����ͼ��ʾ�������ʽ|a+b|-|a-1|+|b+2|��
��֪�������������ϵ�λ����ͼ��ʾ�������ʽ|a+b|-|a-1|+|b+2|�� ��ͼ����ƽ��ֱ������ϵxOy�У�A��BΪx�������㣬C��DΪy���ϵ����㣬������A��C��B�������ߵ�һ����C1�뾭����A��D��B�������ߵ�һ����C2��ϳ�һ��������ߣ����ǰ�����������߳�Ϊ�����ߡ�����֪��C������Ϊ��0��$-\frac{3}{2}$������M��������C2��y=mx2-2mx-3m��m��0���Ķ��㣮
��ͼ����ƽ��ֱ������ϵxOy�У�A��BΪx�������㣬C��DΪy���ϵ����㣬������A��C��B�������ߵ�һ����C1�뾭����A��D��B�������ߵ�һ����C2��ϳ�һ��������ߣ����ǰ�����������߳�Ϊ�����ߡ�����֪��C������Ϊ��0��$-\frac{3}{2}$������M��������C2��y=mx2-2mx-3m��m��0���Ķ��㣮