题目内容
14.如图,是用火柴棍摆成边长分别为1,2,3根火柴棍长的正方形,当边长为n根火柴棍长时,摆出的正方形所用的火柴棍的根数是2n(n+1)(用含n的式子表示,n为正整数).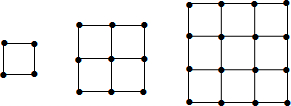
分析 对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.
解答 解:当边长为1根火柴棍时,设摆出的正方形所用的火柴棍的根数为4=2×1×(1+1);
当边长为2根火柴棍时,设摆出的正方形所用的火柴棍的根数为12=2×2×(2+1);
当边长为3根火柴棍时,设摆出的正方形所用的火柴棍的根数为24=2×3×(3+1);
…;
∴当边长为n根火柴棍时,设摆出的正方形所用的火柴棍的根数为2n(n+1).
故答案为:2n(n+1).
点评 本题是一道找规律的题目,这类题型在中考中经常出现,解题的关键是找到图形变化的规律,难度不大.

练习册系列答案
相关题目
4.若x、y互为倒数,则下列等式正确的是( )
| A. | x=-y | B. | xy=-1 | C. | x=$\frac{1}{y}$ | D. | y=±$\frac{1}{x}$ |
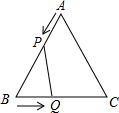 如图所示,已知△ABC是边长为6cm等边三角形,动点P、Q同时从A、B出发,分别在AB、BC方向匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点停止运动,设运动的时间为t (s),解答下列问题:
如图所示,已知△ABC是边长为6cm等边三角形,动点P、Q同时从A、B出发,分别在AB、BC方向匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点停止运动,设运动的时间为t (s),解答下列问题: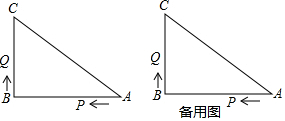
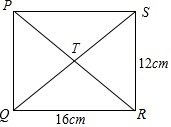 在图中,PQRS是一个长方形.PR与QS相交于T.求:
在图中,PQRS是一个长方形.PR与QS相交于T.求: