题目内容
5.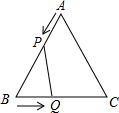 如图所示,已知△ABC是边长为6cm等边三角形,动点P、Q同时从A、B出发,分别在AB、BC方向匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点停止运动,设运动的时间为t (s),解答下列问题:
如图所示,已知△ABC是边长为6cm等边三角形,动点P、Q同时从A、B出发,分别在AB、BC方向匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点停止运动,设运动的时间为t (s),解答下列问题:(1)当t何值时,△PBQ为等边三角形?
(2)当t何值时,△PBQ为直角三角形?
分析 (1)根据等边三角形的判定得:BP=BQ,列等式可得t的值;
(2)分两种情况:①如图2,当∠BQP=90°时,BP=2BQ,则6-t=2×2t,②如图3,当∠BPQ=90°时,BQ=2BP,则2t=2(6-t),分别求出t的值.
解答 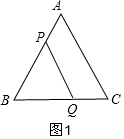 解:(1)由题意得:AP=t,BQ=2t,则BP=6-t,
解:(1)由题意得:AP=t,BQ=2t,则BP=6-t,
∵△ABC是等边三角形,
∴∠B=60°,
当BP=BQ时,△PBQ是等边三角形,如图1,
则6-t=2t,
t=2,
∴当t=2时,△PBQ为等边三角形;
(2)分两种情况: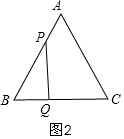
①如图2,当∠BQP=90°时,
∵∠B=60°,
∴∠BPQ=30°,
∴BP=2BQ,
则6-t=2×2t,
t=$\frac{6}{5}$,
②如图3,当∠BPQ=90°时,
∵∠B=60°,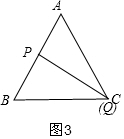
∴∠BQP=30°,
∴BQ=2BP,
2t=2(6-t),
t=3,
由题意得:0≤t≤3,
∴当t=$\frac{6}{5}$或3时,△PBQ为直角三角形.
点评 本题考查了等边三角形的性质和判定、30°角的直角三角形的性质、动点运动问题,本题的关键是熟练掌握等边三角形的性质和判定,要注意直角三角形分情况讨论.

练习册系列答案
相关题目
 在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=-x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点B的坐标为(-1,0).
在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=-x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点B的坐标为(-1,0). 如图所示,∠C=∠D=90°,DB=CA,∠CAB=28°,求∠DAC.
如图所示,∠C=∠D=90°,DB=CA,∠CAB=28°,求∠DAC.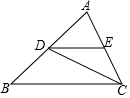 如图,△ABC中,AB=4,点D在AB边上移动(不与A,B重合),DE∥BC,交AC于点E,连接CD,设S△ABC=S,S△DCE=S1.
如图,△ABC中,AB=4,点D在AB边上移动(不与A,B重合),DE∥BC,交AC于点E,连接CD,设S△ABC=S,S△DCE=S1.