题目内容
 如图,在△ABC中,∠A<90°,∠C=30°,AB=4,BC=6,E为AB的中点,P为AC边上一动点,将△ABC绕点B逆时针旋转a角(0°<a≤360°)得到△A1B1C1,点P的对应点为P1,连EP1,在旋转过程中,线段EP1的长度的最小值是( )
如图,在△ABC中,∠A<90°,∠C=30°,AB=4,BC=6,E为AB的中点,P为AC边上一动点,将△ABC绕点B逆时针旋转a角(0°<a≤360°)得到△A1B1C1,点P的对应点为P1,连EP1,在旋转过程中,线段EP1的长度的最小值是( )A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
考点:旋转的性质
专题:计算题
分析:由于E为AB的中点,P1为动点,则当EP1⊥A1C1时,EP1最短,而在△ABC绕点B逆时针旋转(0°<a≤360°)的过程中,当EP1在直线AB上时,EP1最短,然后根据旋转的性质得到∠C1=∠C=30°,BC1=BC=6,再利用含30度的直角三角形三边的关系得到BP1=
BC1=3,而BE=2,所以P1E=BP1-BE=1.
| 1 |
| 2 |
解答: 解:∵E为AB的中点,P1为动点,
解:∵E为AB的中点,P1为动点,
∴当EP1⊥A1C1时,EP1最短,
∵在△ABC绕点B逆时针旋转a角(0°<a≤360°)的过程中,当EP1在直线AB上时,EP1最短,
∴P1点为A1C1与AB垂直时的垂足,EP1最短,如图,
∵△ABC绕点B逆时针旋转a角(0°<a≤360°)得到△A1B1C1,
∴∠C1=∠C=30°,BC1=BC=6,
∴BP1=
BC1=3,
∵AB=4,E为AB的中点,
∴BE=2,
∴P1E=BP1-BE=1.
故选B.
 解:∵E为AB的中点,P1为动点,
解:∵E为AB的中点,P1为动点,∴当EP1⊥A1C1时,EP1最短,
∵在△ABC绕点B逆时针旋转a角(0°<a≤360°)的过程中,当EP1在直线AB上时,EP1最短,
∴P1点为A1C1与AB垂直时的垂足,EP1最短,如图,
∵△ABC绕点B逆时针旋转a角(0°<a≤360°)得到△A1B1C1,
∴∠C1=∠C=30°,BC1=BC=6,
∴BP1=
| 1 |
| 2 |
∵AB=4,E为AB的中点,
∴BE=2,
∴P1E=BP1-BE=1.
故选B.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
相关题目
在实数0、3、-
、2.236、π、3.14中无理数的个数是( )
| 6 |
| A、1 | B、2 | C、3 | D、4 |
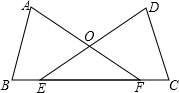 如图,已知AF=DE,AB=DC,BE=CF.求证:(1)△ABF≌△DCE;(2)△EOF是等腰三角形.
如图,已知AF=DE,AB=DC,BE=CF.求证:(1)△ABF≌△DCE;(2)△EOF是等腰三角形. 如图,∠XOY内有一点P,试在射线OX上找出一点M,在射线OY上找出一点N,使PM+MN+NP最短.写出你作图的主要步骤,并标明你所确定的点(要求画出草图,保留作图痕迹).
如图,∠XOY内有一点P,试在射线OX上找出一点M,在射线OY上找出一点N,使PM+MN+NP最短.写出你作图的主要步骤,并标明你所确定的点(要求画出草图,保留作图痕迹).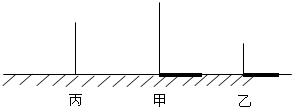 如图所示,甲物体高4米,影长3米,乙物体高2米,影长4米,两物体相距5米.
如图所示,甲物体高4米,影长3米,乙物体高2米,影长4米,两物体相距5米. AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=130°,∠C=30°,则∠DAE的度数是
AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=130°,∠C=30°,则∠DAE的度数是