题目内容
在菱形ABCD中,∠ABC=120°,AB=2cm,点P在对角线AC上,M为AB中点,求△PMB周长的最小值.
考点:轴对称-最短路线问题,菱形的性质
专题:
分析:作出图形,连接BD,先求出∠BAD=60°,然后判断出△ABD是等边三角形,根据菱形的性质,点B、D关于直线AC成轴对称,连接DM,根据轴对称确定最短路线问题可得DM与AC的交点即为使△PMB周长的最小值的点,根据等边三角形的性质求出DM,再求出BM,然后求解即可.
解答: 解:如图,连接BD,
解:如图,连接BD,
∵∠ABC=120°,
∴∠BAD=180°-120°=60°,
∵菱形的邻边AB=AD,
∴△ABD是等边三角形,
∵点B、D关于直线AC成轴对称,
∴连接DM,DM与AC的交点即为使△PMB周长的最小值的点,
∵AB=2cm,M为AB中点,
∴DM=
×2=
cm,
BM=
AB=
×2=1cm,
∴△PMB周长的最小值=(
+1)cm.
 解:如图,连接BD,
解:如图,连接BD,∵∠ABC=120°,
∴∠BAD=180°-120°=60°,
∵菱形的邻边AB=AD,
∴△ABD是等边三角形,
∵点B、D关于直线AC成轴对称,
∴连接DM,DM与AC的交点即为使△PMB周长的最小值的点,
∵AB=2cm,M为AB中点,
∴DM=
| ||
| 2 |
| 3 |
BM=
| 1 |
| 2 |
| 1 |
| 2 |
∴△PMB周长的最小值=(
| 3 |
点评:本题考查了轴对称确定最短路线问题,菱形的性质,等边三角形的判定与性质,熟记各性质并确定出点P的位置是解题的关键,作出图形更形象直观.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是
如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是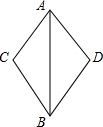 已知:如图,AC=AD,AB是∠CAD的角平分线.求证:BC=BD.
已知:如图,AC=AD,AB是∠CAD的角平分线.求证:BC=BD. 如图,△ABC为等边三角形,D为△ABC内的一点,且BD=DC,∠BDC=90°,已知AB=1,求AD的长.
如图,△ABC为等边三角形,D为△ABC内的一点,且BD=DC,∠BDC=90°,已知AB=1,求AD的长. 如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.∠A=∠D=90°;求证:AB∥DE.
如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.∠A=∠D=90°;求证:AB∥DE. 如图,在△ABC中,点D、E在边BC上,现有①AB=AC,②AD=AE,③BD=CE.请你用其中两个作为条件,余下一个作为结论,编写一道数学问题,并写出解答过程.
如图,在△ABC中,点D、E在边BC上,现有①AB=AC,②AD=AE,③BD=CE.请你用其中两个作为条件,余下一个作为结论,编写一道数学问题,并写出解答过程. 如图,在△ABC中,∠A<90°,∠C=30°,AB=4,BC=6,E为AB的中点,P为AC边上一动点,将△ABC绕点B逆时针旋转a角(0°<a≤360°)得到△A1B1C1,点P的对应点为P1,连EP1,在旋转过程中,线段EP1的长度的最小值是( )
如图,在△ABC中,∠A<90°,∠C=30°,AB=4,BC=6,E为AB的中点,P为AC边上一动点,将△ABC绕点B逆时针旋转a角(0°<a≤360°)得到△A1B1C1,点P的对应点为P1,连EP1,在旋转过程中,线段EP1的长度的最小值是( )