题目内容
用因式分解法解方程:
(1)x2-6x+9=0;
(2)x-3=x(x-3);
(3)x2-12x+20=0;
(4)x2-12x-28=0;
(5)x2-12x+27=0;
(6)x2-12x-13=0.
(1)x2-6x+9=0;
(2)x-3=x(x-3);
(3)x2-12x+20=0;
(4)x2-12x-28=0;
(5)x2-12x+27=0;
(6)x2-12x-13=0.
考点:解一元二次方程-因式分解法
专题:
分析:(1)直接利用完全平方公式分解因式解方程即可;
(2)首先移项,进而利用提取公因式法分解因式解方程即可;
(3)直接利用十字相乘法分解因式解方程即可;
(4)直接利用十字相乘法分解因式解方程即可;
(5)直接利用十字相乘法分解因式解方程即可;
(6)直接利用十字相乘法分解因式解方程即可.
(2)首先移项,进而利用提取公因式法分解因式解方程即可;
(3)直接利用十字相乘法分解因式解方程即可;
(4)直接利用十字相乘法分解因式解方程即可;
(5)直接利用十字相乘法分解因式解方程即可;
(6)直接利用十字相乘法分解因式解方程即可.
解答:解:(1)x2-6x+9=0
(x-3)2=0,
解得:x1=x2=3;
(2)x-3=x(x-3)
(x-3)-x(x-3)=0
(x-3)(1-x)=0
解得:x1=3,x2=1;
(3)x2-12x+20=0
(x-10)(x-2)=0
解得:x1=10,x2=2;
(4)x2-12x-28=0
(x-14)(x+2)=0
解得:x1=14,x2=-2;
(5)x2-12x+27=0
(x-3)(x-9)=0
解得:x1=3,x2=9;
(6)x2-12x-13=0
(x-13)(x+1)=0
解得:x1=13,x2=-1.
(x-3)2=0,
解得:x1=x2=3;
(2)x-3=x(x-3)
(x-3)-x(x-3)=0
(x-3)(1-x)=0
解得:x1=3,x2=1;
(3)x2-12x+20=0
(x-10)(x-2)=0
解得:x1=10,x2=2;
(4)x2-12x-28=0
(x-14)(x+2)=0
解得:x1=14,x2=-2;
(5)x2-12x+27=0
(x-3)(x-9)=0
解得:x1=3,x2=9;
(6)x2-12x-13=0
(x-13)(x+1)=0
解得:x1=13,x2=-1.
点评:此题主要考查了因式分解法解方程,正确分解因式是解题关键.

练习册系列答案
相关题目
 向阳小区计划在一块正方形土地上建一座花坛,园艺师设计了4种不同的图案(如图所示),其中阴影部分用于种植月季花.哪种方案种植月季花的面积最大?
向阳小区计划在一块正方形土地上建一座花坛,园艺师设计了4种不同的图案(如图所示),其中阴影部分用于种植月季花.哪种方案种植月季花的面积最大?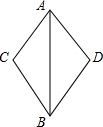 已知:如图,AC=AD,AB是∠CAD的角平分线.求证:BC=BD.
已知:如图,AC=AD,AB是∠CAD的角平分线.求证:BC=BD. 如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.∠A=∠D=90°;求证:AB∥DE.
如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.∠A=∠D=90°;求证:AB∥DE.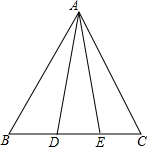 如图,在△ABC中,点D、E在边BC上,现有①AB=AC,②AD=AE,③BD=CE.请你用其中两个作为条件,余下一个作为结论,编写一道数学问题,并写出解答过程.
如图,在△ABC中,点D、E在边BC上,现有①AB=AC,②AD=AE,③BD=CE.请你用其中两个作为条件,余下一个作为结论,编写一道数学问题,并写出解答过程. 如图,在△ABC中,∠A<90°,∠C=30°,AB=4,BC=6,E为AB的中点,P为AC边上一动点,将△ABC绕点B逆时针旋转a角(0°<a≤360°)得到△A1B1C1,点P的对应点为P1,连EP1,在旋转过程中,线段EP1的长度的最小值是( )
如图,在△ABC中,∠A<90°,∠C=30°,AB=4,BC=6,E为AB的中点,P为AC边上一动点,将△ABC绕点B逆时针旋转a角(0°<a≤360°)得到△A1B1C1,点P的对应点为P1,连EP1,在旋转过程中,线段EP1的长度的最小值是( ) 如图所示:正方形网格中的四边形ABCD,若小方格的边长为1,则四边形ABCD的面积是
如图所示:正方形网格中的四边形ABCD,若小方格的边长为1,则四边形ABCD的面积是